题目内容
已知在一个三角形中,若第一个内角的度数是第二个内角的度数的
,第三个内角的度数比这两个内角的度数的和大20°,求这三个内角的度数.
| 3 |
| 2 |
考点:三角形内角和定理
专题:
分析:设第二个内角的度数是x,则第一个内角的度数是
x,第三个内角的度数是x+
x+20°,再根据三角形内角和定理求出x的值即可.
| 3 |
| 2 |
| 3 |
| 2 |
解答:解:设第二个内角的度数是x,则第一个内角的度数是
x,第三个内角的度数是x+
x+20°
∵三角形内角和是180°,
∴x+
x+x+
x+20°=180°,解得x=32°,
∴第一个内角的度数是
×32°=48°;第二个内角的度数是32°;
第三个内角的度数是48°+32°+20°=100°.
| 3 |
| 2 |
| 3 |
| 2 |
∵三角形内角和是180°,
∴x+
| 3 |
| 2 |
| 3 |
| 2 |
∴第一个内角的度数是
| 3 |
| 2 |
第三个内角的度数是48°+32°+20°=100°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
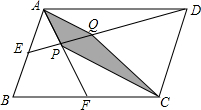 如图,E、F分别是平行四边形ABCD的边AB、BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC,求梯形APCQ的面积与平行四边形ABCD的面积的比值.
如图,E、F分别是平行四边形ABCD的边AB、BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC,求梯形APCQ的面积与平行四边形ABCD的面积的比值.