题目内容
小明有一副三角尺和一个量角器(如图所示).
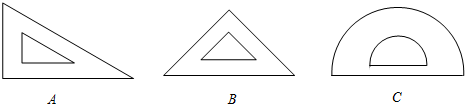
(1)小明的这三件文具中,可以看做是轴对称图形的是 (填字母代号);
(2)请用这三个图形中的两个拼成一个轴对称图案,画出草图(须画出四种);
(3)小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?(请画树状图或列表计算)

(1)小明的这三件文具中,可以看做是轴对称图形的是
(2)请用这三个图形中的两个拼成一个轴对称图案,画出草图(须画出四种);
(3)小红也有同样的一副三角尺和一个量角器.若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?(请画树状图或列表计算)
考点:利用轴对称设计图案,列表法与树状图法
专题:
分析:(1)利用轴对称图形的定义得出即可;
(2)利用轴对称图形的定义得出符合题意的图形即可;
(3)利用列表法得出所有可能,进而利用概率公式求出即可.
(2)利用轴对称图形的定义得出符合题意的图形即可;
(3)利用列表法得出所有可能,进而利用概率公式求出即可.
解答:解:(1)可以看做是轴对称图形的是:B,C;
故答案为:B,C;
(2)如:
 等;
等;
(3)列表如下:
一共有9种结果,每种结果出现的可能性是相同的.而其中能恰好拼成轴对称图形的结果有五种,分别是:
(A,A)、(B,B)、(C,C)、(B,C)、(C,B),
所以两件文具可以拼成一个轴对称图案的概率是
.
故答案为:B,C;
(2)如:
 等;
等;(3)列表如下:
| 小明 小红 | A | B | C |
| A | (A,A) | (A,B) | (A,C) |
| B | (B,A) | (B,B) | (B,C) |
| C | (C,A) | (C,B) | (C,C) |
(A,A)、(B,B)、(C,C)、(B,C)、(C,B),
所以两件文具可以拼成一个轴对称图案的概率是
| 5 |
| 9 |
点评:此题主要考查了利用轴对称设计图案以及列表法求概率,根据定义得出符合题意的图形是解题关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
如果第一个三角形的周长是1,它的三条中位线组成第二个三角形,第二个三角形的三条中位线又组成第三个三角形,依此类推,第2 010个三角形的周长是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
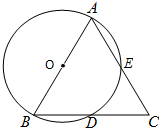 如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.