题目内容
 如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=CE.求∠EBD的度数.
如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=CE.求∠EBD的度数.考点:等腰三角形的性质
专题:
分析:首先∠A=x°,根据∠ABC=90°得到∠C=(90-x)°,利用AB=AD,CE=CB,得到∠ABD=∠ADB,∠BEC=∠EBC,从而得到∠ADB=(
)°=(90-
)°,∠EBC=[180-(90-x)]÷2=[45+
]°,利用∠EBD=∠EBC-∠DBC=(45+
)°-(
)°=45°求解即可.
| 180-x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
| 2 |
解答:解:设∠A=x°,
∵∠ABC=90°,
∴∠C=(90-x)°,
∵AB=AD,CE=CB,
∴∠ABD=∠ADB,∠BEC=∠EBC,
∴∠ADB=(
)°=(90-
)°,∠EBC=[180-(90-x)]÷2=[45+
]°,
∴∠DBC=∠ADB-∠C=(90-
)°-(90-x)°=(
)°,
∴∠EBD=∠EBC-∠DBC=(45+
)°-(
)°=45°,
∵∠ABC=90°,
∴∠C=(90-x)°,
∵AB=AD,CE=CB,
∴∠ABD=∠ADB,∠BEC=∠EBC,
∴∠ADB=(
| 180-x |
| 2 |
| x |
| 2 |
| x |
| 2 |
∴∠DBC=∠ADB-∠C=(90-
| x |
| 2 |
| x |
| 2 |
∴∠EBD=∠EBC-∠DBC=(45+
| x |
| 2 |
| x |
| 2 |
点评:本题考查的是等腰三角形的性质,熟知等腰三角形的两个底角相等是解答此题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点O旋转,若两正方形的边长相等,则两正方形的重合部分的面积( )
如图,正方形ABCD的对角线相交于点O,正方形EFGO绕点O旋转,若两正方形的边长相等,则两正方形的重合部分的面积( )| A、由小变大 |
| B、由大变小 |
| C、始终不变 |
| D、先由大变小,然后又由小变大 |

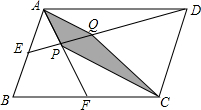 如图,E、F分别是平行四边形ABCD的边AB、BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC,求梯形APCQ的面积与平行四边形ABCD的面积的比值.
如图,E、F分别是平行四边形ABCD的边AB、BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC,求梯形APCQ的面积与平行四边形ABCD的面积的比值.