题目内容
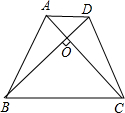如图所示，已知在等腰梯形ABCD中，AD∥BC，AC⊥BD，AB+BC=18，求梯形ABCD的高．考点：等腰梯形的性质
专题：
分析：首先过点D组DE∥AC，交BC延长线于点E，过点D作DH⊥BC于点H，可得BD⊥DE，AC=BD，四边形ACED是平行四边形，即可求得BD与DE的长，继而求得答案．
解答：
解：过点D组DE∥AC，交BC延长线于点E，过点D作DH⊥BC于点H，
∵在等腰梯形ABCD中，AD∥BC，AC⊥BD，
∴BD⊥DE，AC=BD，四边形ACED是平行四边形，
∴CE=AD，DE=AC，
∴BE=BC+CE=BC+AB=18，BD=DE，
∵BD2+DE2=BE2，
∴BD=DE=9
，
∴DH=
=9，
即梯形ABCD的高为9．
解：过点D组DE∥AC，交BC延长线于点E，过点D作DH⊥BC于点H，∵在等腰梯形ABCD中，AD∥BC，AC⊥BD，
∴BD⊥DE，AC=BD，四边形ACED是平行四边形，
∴CE=AD，DE=AC，
∴BE=BC+CE=BC+AB=18，BD=DE，
∵BD2+DE2=BE2，
∴BD=DE=9
| 2 |
∴DH=
| BD•DE |
| BC |
即梯形ABCD的高为9．
点评：此题考查了等腰梯形的性质以及等腰直角三角形的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
如图中的几何体的主视图是（ ）A、 |
B、 |
C、 |
D、 |
在任意三角形ABC边上画正方形ABDE、ACGF，连接BE、FC、EF，并取BE、FC、EF、BC的中点I、J、H、K，连接IH、HJ、JK、IK，求证：HIKJ为正方形．