题目内容
4.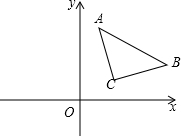 平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).
平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).
分析 求出直线AB的解析式y=-$\frac{1}{2}$x+$\frac{9}{2}$,由于点A和点B到直线CD的距离相等,得到AB∥CD,求得直线CD的解析式为y=-$\frac{1}{2}$x+2,即可得到结果.
解答 解:设直线AB的解析式为:y=kx+b,
∵点A(1,4),点B(5,2),
∴$\left\{\begin{array}{l}{4=k+b}\\{2=5k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{9}{2}}\end{array}\right.$,
∴直线AB的解析式为:y=-$\frac{1}{2}$x+$\frac{9}{2}$,
∵点A和点B到直线CD的距离相等,
∴AB∥CD,
设直线CD的解析式为:y=-$\frac{1}{2}$x+m,
∴1=-$\frac{1}{2}$×2+m,
∴m=2,
∴直线CD的解析式为:y=-$\frac{1}{2}$x+2,
当y=0时,x=4,
∴D的坐标(4,0).
故答案为:(4,0).
点评 本题考查了两直线平行或相交,待定系数法求觳觫的解析式,知道AB∥CD是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.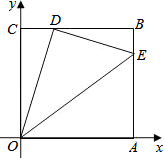 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
 如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )
如图,边长为1的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上,动点D在边BC上移动(不与点B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE,当线段OE的长度取得最小值时,点E的纵坐标为( )| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
 下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.
下图是由14个每相邻两点之间距离为1的点组成的“工”字形图形,请仅用无刻度的直尺通过连接图中的点,根据要求画图.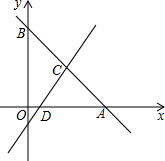 如图,在平面直角坐标系中,直线y=-x+8分别交两轴于点A、B,点C为线段AB的中点,点D在线段OA上,且CD的长是方程$\frac{2}{x+1}=\frac{1}{x-2}$的根.
如图,在平面直角坐标系中,直线y=-x+8分别交两轴于点A、B,点C为线段AB的中点,点D在线段OA上,且CD的长是方程$\frac{2}{x+1}=\frac{1}{x-2}$的根.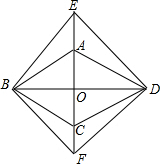 如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.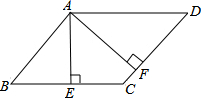 如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.
如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.