题目内容
19．先化简，再求值：2x•$\sqrt{x}$-x2•$\sqrt{\frac{1}{x}}$+$\sqrt{\frac{{x}^{3}}{4}}$，其中x=5．分析 先利用二次根式的性质化简，再进一步代入求得数值即可．
解答 解：原式=2x•$\sqrt{x}$-x•$\sqrt{x}$+$\frac{x}{2}$•$\sqrt{x}$
=$\frac{3}{2}$x$\sqrt{x}$，
当x=5时，
原式=$\frac{15}{2}$$\sqrt{5}$．
点评 此题主要考查的是二次根式的化简求值，注意先化简，再进一步代入求得数值．
练习册系列答案
阅读快车系列答案
相关题目
9．
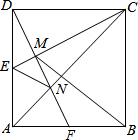如图，正方形ABCD中，E为AD的中点，DF⊥CE于M，交AC于N，交AB于F，连接EN、BM，有如下结论：①△ADF≌△DCE；②MN=FN；③BM=BC；④S△ADN：S四边形CNFB=2：5；⑤∠ADF=∠BMF．其中正确的结论有（ ）
如图，正方形ABCD中，E为AD的中点，DF⊥CE于M，交AC于N，交AB于F，连接EN、BM，有如下结论：①△ADF≌△DCE；②MN=FN；③BM=BC；④S△ADN：S四边形CNFB=2：5；⑤∠ADF=∠BMF．其中正确的结论有（ ）| A． | 5个 | B． | 4个 | C． | 3个 | D． | 2个 |
10．
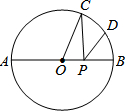如图，已知⊙O的半径为R，C、D是直径AB的同侧圆周上的两点，弧AC的度数为100°弧BC=2弧BD，动点P在线段AB上，则PC+PD的最小值为（ ）
如图，已知⊙O的半径为R，C、D是直径AB的同侧圆周上的两点，弧AC的度数为100°弧BC=2弧BD，动点P在线段AB上，则PC+PD的最小值为（ ）| A． | R | B． | $\sqrt{2}$R | C． | $\sqrt{3}$R | D． | $\frac{\sqrt{5}}{2}$R |
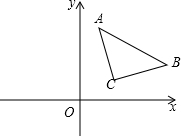平面直角坐标系上点A（1，4），点B（5，2），点C（2，1），若x轴上有一点D，使点A和点B到直线CD的距离相等，那么满足条件的点D的坐标是（4，0）．