题目内容
14.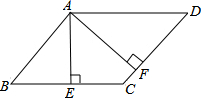 如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.
如图,?ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,∠EAF=45°,则∠BAD=135°.
分析 由AE、AF分别为BC、CD上的高,且∠EAF=45°,即可求得∠C的度数,又由平行四边形的性质,即可求得答案.
解答 解:∵AE、AF分别为BC、CD上的高,
∴∠AEC=∠AFC=90°,
∵∠EAF=45°,
∴∠C=360°-∠EAF-∠AEC-∠AFC=135°,
∵四边形ABCD是平行四边形,
∴∠BAD=∠C=135°,
故答案为:135°.
点评 此题考查了平行四边形的性质.关键是由AE、AF分别为BC、CD上的高,且∠EAF=45°得出∠C的度数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.不等式x-2>1的解集是( )
| A. | x>1 | B. | x>2 | C. | x>3 | D. | x>4 |
8.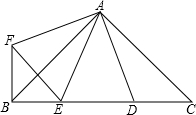 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
 如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )
如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论不正确的是( )| A. | △AED≌△AEF | B. | △ABE∽△ACD | C. | BE+DC>DE | D. | BE2+DC2=DE2 |
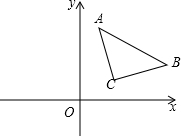 平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).
平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).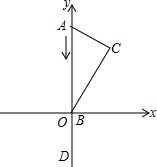 如图,将含30°的直角三角尺放在如图所示的直角坐标系中,点A(0,4),点B在原点,∠C=90°,∠ABC=30°,D点与A点关于原点对称,A点向D点运动,到达D点后停止.B点在x轴上运动.当A到达D时,点C走过的路径长为4$\sqrt{3}$.
如图,将含30°的直角三角尺放在如图所示的直角坐标系中,点A(0,4),点B在原点,∠C=90°,∠ABC=30°,D点与A点关于原点对称,A点向D点运动,到达D点后停止.B点在x轴上运动.当A到达D时,点C走过的路径长为4$\sqrt{3}$.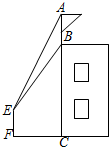 如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,
如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为52°,底部B的仰角为45°,小明的观测点与地面距离EF为1.6m,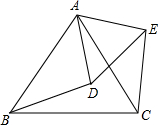 如图,已知△ABC是等边三角形,△ABD绕点A旋转到△ACE的位置,连接DE,若AD=5,求△ADE的周长.
如图,已知△ABC是等边三角形,△ABD绕点A旋转到△ACE的位置,连接DE,若AD=5,求△ADE的周长.