将正方形图1作如下操作:第1次:分别连接各边中点如图2.得到5个正方形,第2次:将图2左上角正方形按上述方法再分割如图3.得到9个正方形-.以此类推.根据以上操作.若要得到821个正方形.则需要操作的次数是205．题目和参考答案——青夏教育精英家教网—

题目内容

3．将正方形图1作如下操作：第1次：分别连接各边中点如图2，得到5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到9个正方形…，以此类推，根据以上操作，若要得到821个正方形，则需要操作的次数是205．

分析由题意可知，第1次：分别连接各边中点如图2，得到4+1=5个正方形；第2次：将图2左上角正方形按上述方法再分割如图3，得到4×2+1=9个正方形…，以此类推，根据以上操作，则第n次得到4n+1个正方形，由此规律代入求得答案即可．

解答解：∵第1次：分别连接各边中点如图2，得到4+1=5个正方形；
第2次：将图2左上角正方形按上述方法再分割如图3，得到4×2+1=9个正方形，
…，
以此类推，根据以上操作，若第n次得到821个正方形，则4n+1=821，
解得：n=205，
故答案为：205．

点评此题主要考查了图形的变化类，根据已知得出正方形个数的变化规律是解题关键．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

14．计算2×（-3）³+4×（-3）的结果等于（　　）

x²+x²=x⁴

a⁰=1

（-3ab²）²=6a²b⁴

18．

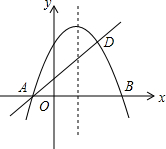如图，抛物线y=-x²+bx+c与x轴交于A、B两点，且B点的坐标为（3，0），经过A点的直线交抛物线于点D（2，3）．
（1）求抛物线的解析式和直线AD的解析式；
（2）过x轴上的点（a，0）作直线EF∥AD，交抛物线于点F，是否存在实数a，使得以A、D、E、F为顶点的四边形是平行四边形？如果存在，求出满足条件的a；如果不存在，请说明理由．

8．

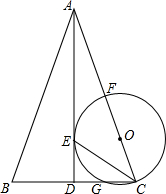如图，△ABC中，AB=AC，AD⊥BC，AD=4，CE平分∠ACB交AD于点E．以线段CE为弦作⊙O，且圆心O落在AC上，⊙O交AC于点F，交BC于点G．
（1）求证：AD与⊙O的相切；
（2）若点G为CD的中点，求⊙O的半径；
（3）判断点E能否为AD的中点，若能则求出BC的长，若不能请说明理由．

15．如图①，在△ABC中，AB=AC，BC=2a（单位：cm），sinB=$\frac{3}{5}$．动点P以1cm/s的速度从点B出发，沿折线B-A-C运动到点C时停止运动．设点P出发x（s）时，△PBC的面积为y（cm²）．已知y与x的函数图象如图②所示，请根据图中信息，解答下列问题：
（1）若a=4时，求图①中AB的长度；
（2）直接写出图②中D点的坐标（$\frac{5}{4}a$，$\frac{3}{4}$a²）；（用含a的代数式表示）
（3）当a为何值时，△ABC∽△DOE．

12．

如图，在△ABC中，∠A=90°，∠B=30°，分别以A、B为圆心，超过AB一半长为半径画弧分别交AB、BC于点D和E，连接AE．则下列说法中不正确的是（　　）

购票人数	50人以下	51～100人	100人以上
票价	13元/人	11元/人	9元/人

某学校七年级1班和2班两个班共104人去游园，其中1班不足50人，2班超过50人．
（1）若以班为单位分别购票，一共应付1240元，求两班各有多少人？
（2）若两班联合购票可少付多少元？

试题分类