题目内容
20. 在△ABC中,∠ACB=90°,AC=12,BC=9,AD=$\frac{1}{3}$AB.
在△ABC中,∠ACB=90°,AC=12,BC=9,AD=$\frac{1}{3}$AB.(1)过点D作出AB的垂线DE,交AC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)求DE的长.
分析 (1)直接利用过一点作已知直线的垂线得出答案;
(2)利用相似三角形的判定与性质得出$\frac{DE}{BC}$=$\frac{AD}{AC}$,进而得出答案.
解答 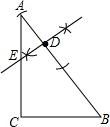 解:(1)如图所示:
解:(1)如图所示:
(2)∵∠A=∠A,∠ADE=∠C=90°,
∴△ADE∽△ACB,
∴$\frac{DE}{BC}$=$\frac{AD}{AC}$,
∵∠ACB=90°,AC=12,BC=9,
∴$\sqrt{{9}^{2}+1{2}^{2}}$=15,
∴AD=$\frac{1}{3}$AB=5,
∴$\frac{DE}{9}$=$\frac{5}{12}$,
∴DE=$\frac{15}{4}$.
点评 此题主要考查了复杂作图以及相似三角形的判定与性质,正确得出△ADE∽△ACB是解题关键.

练习册系列答案
相关题目
10.下列运算中,正确的是( )
| A. | 2xa+xa=3x2a2 | B. | (a2)3=a6 | C. | 3a•2a=6a | D. | 3-2=-6 |
11.下列各运算中,计算正确的是( )
| A. | x2+x2=x4 | B. | $\sqrt{9}$=3 | C. | a0=1 | D. | (-3ab2)2=6a2b4 |
12. 如图,在△ABC中,∠A=90°,∠B=30°,分别以A、B为圆心,超过AB一半长为半径画弧分别交AB、BC于点D和E,连接AE.则下列说法中不正确的是( )
如图,在△ABC中,∠A=90°,∠B=30°,分别以A、B为圆心,超过AB一半长为半径画弧分别交AB、BC于点D和E,连接AE.则下列说法中不正确的是( )
 如图,在△ABC中,∠A=90°,∠B=30°,分别以A、B为圆心,超过AB一半长为半径画弧分别交AB、BC于点D和E,连接AE.则下列说法中不正确的是( )
如图,在△ABC中,∠A=90°,∠B=30°,分别以A、B为圆心,超过AB一半长为半径画弧分别交AB、BC于点D和E,连接AE.则下列说法中不正确的是( )| A. | DE是AB的中垂线 | B. | ∠AED=60° | C. | AE=BE | D. | S△DAE:S△AEC=1:3 |
9.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | a(a+b)=a2+ab | C. | -2(a-1)=-2a-2 | D. | 3a2-2a2=1 |
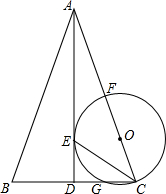 如图,△ABC中,AB=AC,AD⊥BC,AD=4,CE平分∠ACB交AD于点E.以线段CE为弦作⊙O,且圆心O落在AC上,⊙O交AC于点F,交BC于点G.
如图,△ABC中,AB=AC,AD⊥BC,AD=4,CE平分∠ACB交AD于点E.以线段CE为弦作⊙O,且圆心O落在AC上,⊙O交AC于点F,交BC于点G.