题目内容
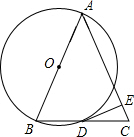已知：如图，AB=AC，AB是⊙O的直径，⊙O交BC于D，DE⊥AC．求证：DE是⊙O的切线．考点：切线的判定
专题：证明题
分析：首先连接AD，DO，进而利用圆周角定理以及等腰三角形的性质和三角形中位线定理求出DO∥AC，进而得出即可．
解答：
证明：连接AD，DO，
∵AB是⊙O的直径，
∴∠ADB=90°，
∵AB=AC，
∴BD=CD，
∵AO=BO，
∴DO是△ABC的中位线，
∴DO∥AC，
∵DE⊥AC
∴OD⊥DE，
∴DE是⊙O的切线．
证明：连接AD，DO，∵AB是⊙O的直径，
∴∠ADB=90°，
∵AB=AC，
∴BD=CD，
∵AO=BO，
∴DO是△ABC的中位线，
∴DO∥AC，
∵DE⊥AC
∴OD⊥DE，
∴DE是⊙O的切线．
点评：此题主要考查了切线的判定以及圆周角定理以及等腰三角形的性质和三角形中位线定理等知识，得出DO∥AC是解题关键．
练习册系列答案
相关题目
△ABC和△FED中，AD=FC，∠A=∠F．当添加条件
某校针对某事件在本校学生中做了一次抽样调查，并把调查结果分为三种类型：
用16m长的铝合金条制成如图所示的矩形窗框，CD长表示窗框的宽，EF=0.5m．（铝合金条的宽度忽略不计）