题目内容
 用16m长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5m.(铝合金条的宽度忽略不计)
用16m长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5m.(铝合金条的宽度忽略不计)(1)求窗框的透光面积S(m2)与窗框的宽x(m)之间的函数关系式;
(2)如何设计才能使窗框的透光面积最大?最大面积为多少?
(3)当窗框的面积不小于7m2时,试结合函数的图象,直接写出x的取值范围.
考点:二次函数的应用
专题:
分析:(1)可证明四边形BCHG、四边形DEGH、四边形ABEF是矩形.由图得出BC以及AC,从而得出用含x的代数式表示S即可;
(2)根据(1)关系式利用公式法求出最值即可,
(3)根据当s=10时解方程即可得出图象上点的坐标,进而求出与x轴交点坐标,得出图象即可得出x的取值范围.
(2)根据(1)关系式利用公式法求出最值即可,
(3)根据当s=10时解方程即可得出图象上点的坐标,进而求出与x轴交点坐标,得出图象即可得出x的取值范围.
解答:解:(1)在矩形ACDF中,∵∠A=90°,AB∥EF,AF∥BE,
∴四边形ABEF是矩形,
∴EF=AB=0.5米.GH⊥CD,
∴∠CHG=90°=∠C=∠CBG,
∴四边形BCHG是矩形,同理四边形DEGH是矩形.
设AF=x,
∵BC=HG=DE=
=5-x,AC=BC+AB,
∴y=5-x+0.5=-x+
.
S=xy=(-x+
)x=-x 2+
x(0<x<
),
(2)依题意得S=-x 2+
x,
当x=-
=-
=
时,
S最大=
=
=
cm2;
(3)当(-x+
)x=7,
解得x1=
,x2=4,
当s=0,则0=-x 2+
x,
解得:x1=0,x2=5.5,
图象与x轴交点坐标为:(0,0),(5.5,0),再利用图象顶点坐标为:(
,
),
如图所示:

由图象得出x的取值范围:3.5≤x≤4.
∴四边形ABEF是矩形,
∴EF=AB=0.5米.GH⊥CD,
∴∠CHG=90°=∠C=∠CBG,
∴四边形BCHG是矩形,同理四边形DEGH是矩形.
设AF=x,
∵BC=HG=DE=
| 16-2×0.5-3x |
| 3 |
∴y=5-x+0.5=-x+
| 11 |
| 2 |
S=xy=(-x+
| 11 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
(2)依题意得S=-x 2+
| 11 |
| 2 |
当x=-
| b |
| 2a |
| ||
| 2×(-1) |
| 11 |
| 4 |
S最大=
| 4ac-b2 |
| 4a |
0-
| ||
| 4×(-1) |
| 121 |
| 16 |
(3)当(-x+
| 11 |
| 2 |
解得x1=
| 7 |
| 2 |
当s=0,则0=-x 2+
| 11 |
| 2 |
解得:x1=0,x2=5.5,
图象与x轴交点坐标为:(0,0),(5.5,0),再利用图象顶点坐标为:(
| 11 |
| 4 |
| 121 |
| 16 |
如图所示:

由图象得出x的取值范围:3.5≤x≤4.
点评:本题考查了二次函数的应用,利用了二次函数的顶点坐标,由图象得出x的取值范围是解题关键.

练习册系列答案
相关题目
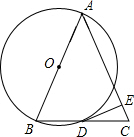 已知:如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DE⊥AC.求证:DE是⊙O的切线.
已知:如图,AB=AC,AB是⊙O的直径,⊙O交BC于D,DE⊥AC.求证:DE是⊙O的切线.