题目内容
8.等边△ABC内有一点P,P点到3边的距离分别为1、2、3,该等边三角形的边长为a,则S△ABC=12$\sqrt{3}$.分析 先连接AP、BP、CP,过点A作AD⊥BC于D,根据S△ABC=$\frac{1}{2}$BC•(PQ+PR+PS)=$\frac{1}{2}$BC•AD得出PQ+PS+PR=AD,由直角三角形的性质可得出BC的值,进而可得出△ABC的面积.
解答 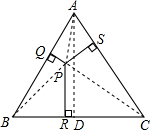 解:连接AP、BP、CP,过点A作AD⊥BC于D,
解:连接AP、BP、CP,过点A作AD⊥BC于D,
∵S△ABC=$\frac{1}{2}$BC•(PQ+PR+PS)=$\frac{1}{2}$BC•AD,
∴PQ+PR+PS=AD,
∴AD=1+2+3=6,
∵∠ABC=60°
∴AB=6×$\frac{2}{\sqrt{3}}$=4$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×4$\sqrt{3}$=12$\sqrt{3}$,
故答案为:12$\sqrt{3}$.
点评 本题考查的是等边三角形的性质及三角形的面积公式,根据题意作出辅助线,得出PQ+PR+PS=AD是解答此题的关键.

练习册系列答案
相关题目
19.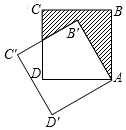 如图,边长为2的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
如图,边长为2的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
 如图,边长为2的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )
如图,边长为2的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为( )| A. | 2 | B. | $\frac{3\sqrt{3}}{2}$ | C. | 4-$\frac{4\sqrt{3}}{3}$ | D. | 4-$\frac{3\sqrt{3}}{4}$ |
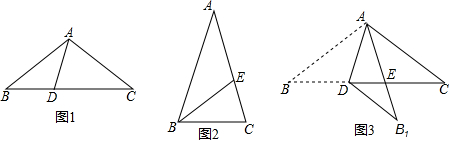
 在如图所示的正方形网格中,每个小正方形的边长均为1,△ABC的顶点A、C的坐标分别为(-4,5),(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,△ABC的顶点A、C的坐标分别为(-4,5),(-1,3). 在一节数学课上,老师布置了一个任务:
在一节数学课上,老师布置了一个任务: