题目内容
12.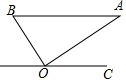 如图,在 Rt△ABO 中,斜边 AB=1,若 OC∥BA,∠AOC=36°,则下面四个结论:
如图,在 Rt△ABO 中,斜边 AB=1,若 OC∥BA,∠AOC=36°,则下面四个结论:①点B到AO的距离为sin54°;②点B到AO的距离为tan36°;
③点A到OC的距离为sin36°•sin54°;④点A到OC的距离为cos36°•sin54°.
其中正确的是③(填序号).
分析 过点A作BH⊥OC于H,在Rt△AOB中,利用正弦和余弦的定义可计算出OB和OA,则可对①②进行判断;在Rt△OBH中,利用∠BOH的正弦可计算出BH,然后关键平行线的性质可对③④进行判断.
解答 解: 在Rt△AOB中,∵sinA=$\frac{BO}{AB}$,
在Rt△AOB中,∵sinA=$\frac{BO}{AB}$,
∴BO=ABsinA=sin36°或BO=cos54°,
即点B到OA的距离为sin36°或cos54°,所以①错误;
∵cosA=$\frac{OA}{AB}$,
∴OA=ABcosA=cos36°或sin54°,
即点A到OB的距离为cos36°或sin54°,所以②错误;
过点A作BH⊥OC于H,如图,
在Rt△OBH中,∵sin∠BOH=$\frac{BH}{OB}$,
∴BH=OBsin54°=sin36°•sin54°,
∵OC∥AB,
∴点A到OC的距离为sin36°•sin54°.所以③正确,而④错误.
故答案为:③.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形,熟练掌握勾股定理和锐角三角函数的定义是解决此类问题的关键.直线外一点到直线的垂线段的长度,叫做点到直线的距离.

练习册系列答案
相关题目

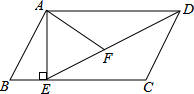 如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.