题目内容
20.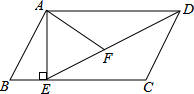 如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在?ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)试说明:△ADF∽△DEC;
(2)若AB=7,AD=12,AE=5,求AF的长.
分析 (1)根据四边形ABCD为平行四边形,利用平行四边形的对边平行且相等,得到一对同旁内角互补,一对内错角相等,根据已知角相等,利用等角的补角相等得到三角形ADF与三角形DEC相似,利用相似三角形对应边成比例即可得证;
(2)根据AE与BC垂直,得到两个角为直角,利用勾股定理求出BE与DE的长,由三角形ADF与三角形DEC相似,得比例,求出AF的长即可.
解答 (1)证明:∵平行四边形ABCD,∠AFE=∠B,
∴AB∥CD,AD∥BC,AD=BC,
∴∠B+∠C=180°,∠ADF=∠CED,
∵∠AFD+∠AFE=180°,
∴∠C=∠AFD,
∴△ADF∽△DEC;
(2)解:∵AE⊥BC,
∴∠AEB=∠AEC=90°,
在Rt△ABE中,根据勾股定理得:BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=2$\sqrt{6}$,EC=12-2$\sqrt{6}$,
在Rt△ADE中,根据勾股定理得:DE=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∵△ADF∽△DEC,
∴$\frac{AD}{DE}$=$\frac{AF}{DC}$,
∴AF=$\frac{84}{13}$.
点评 此题考查了相似三角形的判定与性质,以及平行四边形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
8.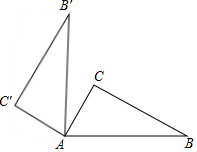 如图,将△ABC绕点A逆时针旋转得到△AB′C′,若∠CAC′=80°,则∠BAB′的度数为( )
如图,将△ABC绕点A逆时针旋转得到△AB′C′,若∠CAC′=80°,则∠BAB′的度数为( )
 如图,将△ABC绕点A逆时针旋转得到△AB′C′,若∠CAC′=80°,则∠BAB′的度数为( )
如图,将△ABC绕点A逆时针旋转得到△AB′C′,若∠CAC′=80°,则∠BAB′的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 80° |
5.方程3x-7=5的解是( )
| A. | x=2 | B. | x=3 | C. | x=4 | D. | x=5 |
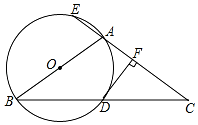 如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.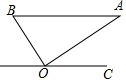 如图,在 Rt△ABO 中,斜边 AB=1,若 OC∥BA,∠AOC=36°,则下面四个结论:
如图,在 Rt△ABO 中,斜边 AB=1,若 OC∥BA,∠AOC=36°,则下面四个结论: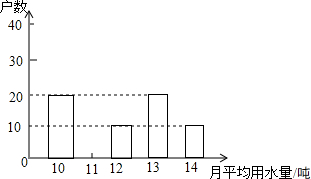 为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量 (单位:吨),并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量 (单位:吨),并将调查结果制成了如图所示的条形统计图. 如图,矩形OABC在平面直角坐标系xoy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O、A两点,直线AC交抛物线于点D(1,n).
如图,矩形OABC在平面直角坐标系xoy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O、A两点,直线AC交抛物线于点D(1,n).