题目内容
5.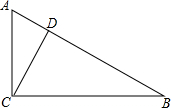 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;
如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;(1)求证:CD⊥AB;
(2)在(1)中画△ABC的角平分线AE,交CD于点F,试判断∠AEC和∠CFE的数量关系,并加以证明.
分析 (1)根据直角三角形的两锐角互余可得:∠A+∠B=90°,则∠A+∠ACD=90°,由三角形内角和及垂直定义可得结论;
(2)画图,根据等角的余角相等可得:∠AEC=∠CFE.
解答 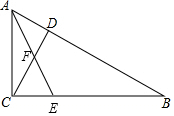 证明:(1)∵∠ACB=90°,
证明:(1)∵∠ACB=90°,
∴∠A+∠B=90°,
∵∠ACD=∠B,
∴∠A+∠ACD=90°,
∴∠ADC=90°,
∴CD⊥AB;
(2)如图所示,
∠AEC=∠CFE,理由是:
∵AE平分∠CAB,
∴∠CAE=∠BAE,
∵∠ADC=90°,
∴∠BAE+∠AFD=90°,
∵∠ACB=90°,
∴∠CAE+∠AEC=90°,
∴∠AEC=∠AFD,
∵∠AFD=∠CFE,
∴∠AEC=∠CFE.
点评 本题考查了三角形内角和定理、直角三角形的性质、垂直的定义及余角的性质,属于基础题,熟练掌握同角或等角的余角相等是关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
16.如果一个三角形的三条高的交点恰好是三角形的一个顶点,则这个三角形的形状一定是( )
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 直角三角形 |
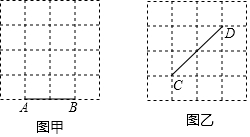
17.在方格纸中,每个方格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.如图甲中,每个小正方形的边长为1,以线段AB为一边的格点三角形随着第三个顶点的位置不同而发生变化.
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值.
(2)在图乙中,所给的方格纸大小与甲图一样,如果以线段CD为一边,做格点三角形,试填写下表,并计算出格点三角形面积的平均值.
(3)如果将图乙中格点三角形的面积用y来表示,频数用x来表示,根据你所填写的数据,猜想y与x之间存在何种函数关系?并求出该函数关系.
(1)根据图甲,填写下表,并计算出格点三角形面积的平均值.
| 格点三角形面积 | 1 | 2 | 3 | 4 |
| 频数 | 5 | 5 | 5 | 5 |
(3)如果将图乙中格点三角形的面积用y来表示,频数用x来表示,根据你所填写的数据,猜想y与x之间存在何种函数关系?并求出该函数关系.

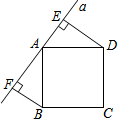 如图所示,直线经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E.若DE=5,BF=3,则EF的长为8.
如图所示,直线经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E.若DE=5,BF=3,则EF的长为8.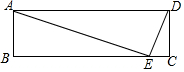 如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n.且m,n满足m=$\sqrt{n-8}$+$\sqrt{16-2n}$+2.则BE的长为15.
如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n.且m,n满足m=$\sqrt{n-8}$+$\sqrt{16-2n}$+2.则BE的长为15.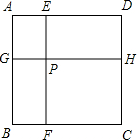 如图,边长为a的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形,EF与GH交于点P,连接AF、AH.
如图,边长为a的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形,EF与GH交于点P,连接AF、AH.