题目内容
10.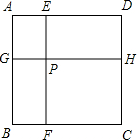 如图,边长为a的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形,EF与GH交于点P,连接AF、AH.
如图,边长为a的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形,EF与GH交于点P,连接AF、AH.(1)若BF=DH,求证:AF=AH.
(2)若∠FAH=45°,求△FCH的周长(用含a的代数式表示).
(3)若Rt△GBF的周长为a,求矩形EPHD的面积(用含a的代数式表示).
分析 (1)因为BF=DH⇒BF=AE,由AB=AD,∠ABC=∠ADH⇒△ABF≌△ADH(SAS);
(2)将△ADH绕点A顺时针旋转90°后,可得△AFH≌△AFM然后可求得结论;
(3)设BF=x,GB=y,根据线段之间的关系利用勾股定理求出xy的值;
解答 (1)证明:连接AH、AF.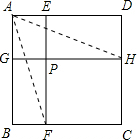
∵ABCD是正方形,
∴AD=AB,∠D=∠B=90°.
∵ADHG与ABFE都是矩形,
∴DH=AG,AE=BF,
又∵BF=DH,
∴AE=BF.
在Rt△ADH与Rt△ABF中,
∵AD=AB,∠D=∠B=90°,DH=BF,
∴Rt△ADH≌Rt△ABF,
∴AF=AH.
(2)证明:将△ADH绕点A顺时针旋转90°到△ABM的位置.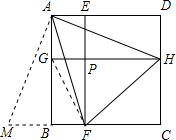
在△AMF与△AHF中,
∵AM=AH,AF=AF,
∠MAF=∠MAH-∠FAH=90°-45°=45°=∠FAH,
∴△AMF≌△AHF.
∴MF=HF.
∵MF=MB+BF=HD+BF,
∴△FCH的周长=CF+FH+CH=CF+BF+CH+DH=2a.
(3)解:设BF=x,GB=y,则FC=a-x,AG=a-y,(0<x<1,0<y<1)
在Rt△GBF中,GF2=BF2+BG2=x2+y2
∵Rt△GBF的周长为a,
∴BF+BG+GF=x+y+$\sqrt{{x}^{2}+{y}^{2}}$=a,
即 $\sqrt{{x}^{2}+{y}^{2}}$=a-(x+y)
即x2+y2=a2-2a(x+y)+(x+y)2
整理得2xy-2ax-2ay+a2=0
∴xy-ax-ay=-$\frac{1}{2}$a2,
∴矩形EPHD的面积S=PH•EP=FC•AG=(a-x)(a-y)=xy-ax-ay+a2=-$\frac{1}{2}$a2+a2=$\frac{1}{2}$a2.
点评 本题考查正方形的性质、勾股定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | 6 | B. | -6 | C. | 8 | D. | -8 |
| A. | $\frac{15}{64}$ | B. | $\frac{1}{4}$ | C. | $\frac{13}{48}$ | D. | $\frac{1}{3}$ |
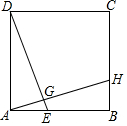 如图,正方形ABCD中,H在BC上,DE⊥AH交AB于点E,交AH于点G,若AB=3,BH=1.
如图,正方形ABCD中,H在BC上,DE⊥AH交AB于点E,交AH于点G,若AB=3,BH=1.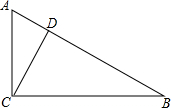 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;
如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B;