题目内容
17.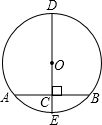 如图,DE是⊙O的直径,弦AB⊥DE,垂足为C,若AB=8,OC=3.求⊙O的半径.
如图,DE是⊙O的直径,弦AB⊥DE,垂足为C,若AB=8,OC=3.求⊙O的半径.
分析 先根据垂径定理得出BC的长,再在Rt△OBC中利用勾股定理求出OB的长即可.
解答 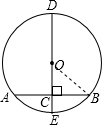 解:连接OB,
解:连接OB,
∵DE是⊙O的直径,弦AB⊥DE,AB=8,
∴BC=$\frac{1}{2}$AB=4,
∵0C=3,
∴在Rt△OBC中,OB=$\sqrt{O{C}^{2}+B{C}^{2}}$=5.
∴⊙O的半径为5.
点评 本题考查的是垂径定理及勾股定理,先求出BC的长,再利用勾股定理求出OB的长是解答此题的关键.

练习册系列答案
相关题目
12.抛物线y=x2-2的顶点坐标为( )
| A. | (0,-2) | B. | (-2,0) | C. | (0,2) | D. | (2,0) |
2.下列图形中,既是中心对称图形又是有且只有两条对称轴的对称图形是( )
| A. | 正三角形 | B. | 正方形 | C. | 圆 | D. | 矩形 |
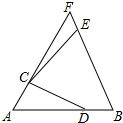 如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.
如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.
 如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:∠DCE=∠MDF(答案不唯一).
如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:∠DCE=∠MDF(答案不唯一).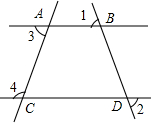 如图,直线AB、CD分别与直线AC相交于点A、C,与直线BD相交于点B、D.若∠1=∠2,∠3=72°,求∠4的度数.
如图,直线AB、CD分别与直线AC相交于点A、C,与直线BD相交于点B、D.若∠1=∠2,∠3=72°,求∠4的度数.