题目内容
14.化简,再求值.($\sqrt{x}$-$\frac{x}{x+\sqrt{x}}$)÷$\frac{x-\sqrt{x}}{\sqrt{x}}$,其中x=2+$\sqrt{2}$.分析 首先对括号内的式子进行通分相减,然后把除法转化为乘法,进行乘法运算即可化简,然后代入数值进行分母有理化即可求解.
解答 解:原式=$\frac{\sqrt{x}(x+\sqrt{x})-x}{x+\sqrt{x}}$•$\frac{\sqrt{x}}{x-\sqrt{x}}$
=$\frac{x\sqrt{x}}{x+\sqrt{x}}$•$\frac{\sqrt{x}}{x-\sqrt{x}}$
=$\frac{{x}^{2}}{{x}^{2}-x}$
=$\frac{x}{x-1}$,
当x=2+$\sqrt{2}$时,原式=$\frac{2+\sqrt{2}}{2+\sqrt{2}-1}$=$\frac{2+\sqrt{2}}{1+\sqrt{2}}$=(2+$\sqrt{2}$)($\sqrt{2}$-1)=$\sqrt{2}$.
点评 本题考查的根式的化简求值,正确对已知的根式进行混合运算是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
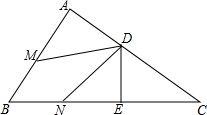 如图所示,已知:△ABC中,∠A=90°,D是AC上一点,DE⊥BC,垂足为E,点M、N分别在BA、BC上,且BM=BN,DM=DN,求证:DA=DE.
如图所示,已知:△ABC中,∠A=90°,D是AC上一点,DE⊥BC,垂足为E,点M、N分别在BA、BC上,且BM=BN,DM=DN,求证:DA=DE.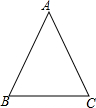 如图,等腰△ABC中,AB=AC.
如图,等腰△ABC中,AB=AC. 已知:⊙O的半径是3,AB是⊙O的一条直径,CD是弦,且CD∥AB.若∠DAC=20°,则图中阴影部分的面积为π.
已知:⊙O的半径是3,AB是⊙O的一条直径,CD是弦,且CD∥AB.若∠DAC=20°,则图中阴影部分的面积为π. 如图是长方体的展开图,那么这个长方体的A面的对面是F面,B面的对面是D面,C面的对面是E面.
如图是长方体的展开图,那么这个长方体的A面的对面是F面,B面的对面是D面,C面的对面是E面.