题目内容
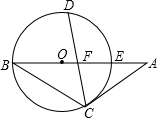 如图,以△ABC的边AB上一点O为圆心的圆经过B、C两点,且与边AB相交于点E,D是弧BE的中点,CD交AB于F,AC=AF.
如图,以△ABC的边AB上一点O为圆心的圆经过B、C两点,且与边AB相交于点E,D是弧BE的中点,CD交AB于F,AC=AF.(1)求证:AC是⊙O的切线;
(2)若EF=5,DF=
| 37 |
考点:切线的判定
专题:证明题
分析:(1)连结OD、OC,如图,根据垂径定理的推论,由D是弧BE的中点得到OD⊥BE,则∠D+∠3=90°,而∠3=∠2,所以∠D+∠2=90°,再利用AF=AC,OD=OC,得到∠1=∠2,∠D=∠4,易得∠1+∠4=90°,于是根据切线的判定定理即可得到AC是⊙O的切线;
(2)设⊙O的半径为r,则OF=OE-EF=r-5,在Rt△ODF中,根据勾股定理得r2+(r-5)2=(
)2,然后解方程即可得到圆的半径.
(2)设⊙O的半径为r,则OF=OE-EF=r-5,在Rt△ODF中,根据勾股定理得r2+(r-5)2=(
| 37 |
解答: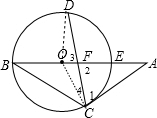 (1)证明:连结OD、OC,如图,
(1)证明:连结OD、OC,如图,
∵D是弧BE的中点,
∴OD⊥BE,
∴∠D+∠3=90°,
∵∠3=∠2,
∴∠D+∠2=90°,
∵AF=AC,OD=OC,
∴∠1=∠2,∠D=∠4,
∴∠1+∠4=90°,
∴OC⊥AC,
∴AC是⊙O的切线;
(2)解:设⊙O的半径为r,
则OF=OE-EF=r-5,
在Rt△ODF中,
∵OD2+OF2=DF2,
∴r2+(r-5)2=(
)2,
整理得r2-5r-6=0,
解得r1=6,r2=-1,
∴,⊙O的半径为6.
 (1)证明:连结OD、OC,如图,
(1)证明:连结OD、OC,如图,∵D是弧BE的中点,
∴OD⊥BE,
∴∠D+∠3=90°,
∵∠3=∠2,
∴∠D+∠2=90°,
∵AF=AC,OD=OC,
∴∠1=∠2,∠D=∠4,
∴∠1+∠4=90°,
∴OC⊥AC,
∴AC是⊙O的切线;
(2)解:设⊙O的半径为r,
则OF=OE-EF=r-5,
在Rt△ODF中,
∵OD2+OF2=DF2,
∴r2+(r-5)2=(
| 37 |
整理得r2-5r-6=0,
解得r1=6,r2=-1,
∴,⊙O的半径为6.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.

练习册系列答案
相关题目
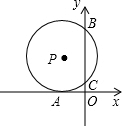 如图,⊙P的圆心在第二象限内,且与x轴相切于点A,与y轴相交于B(0,8)、C(0,2),则圆心P的坐标是( )
如图,⊙P的圆心在第二象限内,且与x轴相切于点A,与y轴相交于B(0,8)、C(0,2),则圆心P的坐标是( )| A、(-3,4) |
| B、(-4,6) |
| C、(-3,5) |
| D、(-4,5) |
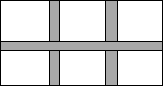 新园小区计划在一块长为40米,宽为26米的矩形场地上修建三条同样宽的甬路(两条纵向、一条横向,且横向、纵向互相垂直),其余部分种花草.若要使种花草的面积达到800m2,则甬路宽为多少米?设甬路宽为x米,则根据题意,可列方程为
新园小区计划在一块长为40米,宽为26米的矩形场地上修建三条同样宽的甬路(两条纵向、一条横向,且横向、纵向互相垂直),其余部分种花草.若要使种花草的面积达到800m2,则甬路宽为多少米?设甬路宽为x米,则根据题意,可列方程为 如图,在△ABC中,D、E分别是边AC和AB上的点,且DE≠BC,请你添加一个条件,使得△ABC与△AED相似,你添加的条件是
如图,在△ABC中,D、E分别是边AC和AB上的点,且DE≠BC,请你添加一个条件,使得△ABC与△AED相似,你添加的条件是 如图,已知点A的坐标为(-2,2),点B的坐标为(-1,-3),则点C的坐标是
如图,已知点A的坐标为(-2,2),点B的坐标为(-1,-3),则点C的坐标是 如图,在万三中的“创造节”上,数学兴趣小组长小明想要知道旗杆的直径.苦于身边没有直尺和测量工具,只有一根已知长为30厘米的细线,他用这个细线刚好将旗杆缠了三圈,每缠一圈,细线上升6厘米,请你帮助小明算出旗杆的直径是
如图,在万三中的“创造节”上,数学兴趣小组长小明想要知道旗杆的直径.苦于身边没有直尺和测量工具,只有一根已知长为30厘米的细线,他用这个细线刚好将旗杆缠了三圈,每缠一圈,细线上升6厘米,请你帮助小明算出旗杆的直径是