题目内容
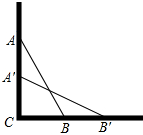一架云梯AB长25米，如图那样斜靠在一面墙AC上，这时云梯底端B离墙底C的距离BC为7米．（1）这云梯的顶端距地面AC有多高？
（2）如果云梯的顶端A下滑了4米，那么它的底部B在水平方向向右滑动了多少米？
考点：勾股定理的应用
专题：
分析：（1）在直角三角形ABC中，利用勾股定理即可求出AC的长；
（2）首先求出AC的长，利用勾股定理可求出B′C的长，进而得到BB′=CB′-CB的值．
（2）首先求出AC的长，利用勾股定理可求出B′C的长，进而得到BB′=CB′-CB的值．
解答：解：（1）在Rt△ABC中，由勾股定理得AC2+BC2=AB2，
即AC2+72=252，
所以AC=24（m），
即这架云梯的顶端A距地面有24m高；
（2）梯子的底端在水平方向也滑动了8m．
理由：∵云梯的顶端A下滑了4m至点A，
∴AC=AC-A′A=24-4=20（m），
在Rt△ACB′中，由勾股定理得AC2+BC′2=AB′2，
即202+B′C2=252
所以B′C=15（m）
BB′=CB′-BB=15-7=8（m），
即梯子的底端在水平方向也滑动了8m．
即AC2+72=252，
所以AC=24（m），
即这架云梯的顶端A距地面有24m高；
（2）梯子的底端在水平方向也滑动了8m．
理由：∵云梯的顶端A下滑了4m至点A，
∴AC=AC-A′A=24-4=20（m），
在Rt△ACB′中，由勾股定理得AC2+BC′2=AB′2，
即202+B′C2=252
所以B′C=15（m）
BB′=CB′-BB=15-7=8（m），
即梯子的底端在水平方向也滑动了8m．
点评：本题考查了勾股定理在实际生活中的应用，本题中根据梯子长不会变的等量关系求解是解题的关键．
练习册系列答案
相关题目
如图所示，PA、PB为⊙O的切线，M、N是PA、AB的中点，连接MN交⊙O点C，连接PC交⊙O于D，连接ND交PB于Q，求证：MNQP为菱形．
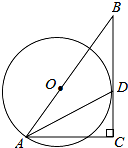如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB=6，延长BO交⊙O于点A，点D为⊙O上一点，过点A作直线BD的垂线，垂足为C，AD平分∠BAC．（1）求证：BC是⊙O的切线；
（2）求AC的长．
如图，在△ABC中，D、E分别是边AC和AB上的点，且DE≠BC，请你添加一个条件，使得△ABC与△AED相似，你添加的条件是下列各式中，不是最简二次根式的是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，一次函数y=-