��Ŀ����
9����ͼ?��ʾ�����ĸ�ͬ����С��ֱ�������Σ�����ֱ�DZ߷ֱ�Ϊa��b��б��Ϊc��ƴ��һ�������Σ��м�����һ��С�����Σ���1����������֮��������ϵ��̽��������a��b��c�ĵ�ʽ��
��2�����ã�1���з��ֵ�ֱ������������ֱ�DZ�a��b��б��c֮��Ĺ�ϵ��������⣺��ͼ?����ֱ�ǡ�ABC�У���C=90�㣬��c=6��a+b=8�����ABC�����Ϊ7��
��3����ͼ�ۣ��������εı߳�Ϊm��С�����εı߳�Ϊn������x��y��ʾ�ĸ����ε����߳���x��y�����۲�ͼ����ָ�����¹�ϵʽ��
��1��xy=$\frac{{m}^{2}-{n}^{2}}{4}$ ��2��x+y=m ��3��x2-y2=m•n��4��x2+y2=$\frac{{m}^{2}+{n}^{2}}{2}$ ������ȷ���У�1����2����3����4��������ţ�
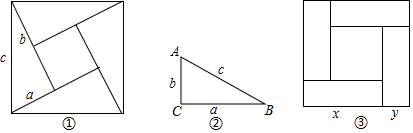
���� ��1�����ݴ������ε�����IJ�ͬ��ʾ���������ɵõ���a��b��c�ĵ�ʽ��
��2�����ݣ�a+b��2=64��a2+b2=c2=36�����ɵõ�ab=14�������ó���ABC�������
��3��������ȫƽ����ʽ�Լ�ƽ���ʽ�����ɵõ�xy��x+y��x2-y2�Լ�x2+y2֮���������ϵ�������ó���ȷ���ۣ�
��� �⣺��1���������ε����=c2��
����������=4��$\frac{1}{2}$ab+��b-a��2��
��4��$\frac{1}{2}$ab+��b-a��2=c2��
��2ab+b2-2ab+a2=c2��
��a2+b2=c2
��2����a+b=8��
�ࣨa+b��2=64����a2+2ab+b2=64��
�֡�a2+b2=c2=36��
��2ab=64-36=28����ab=14��
���ABC�����Ϊ$\frac{1}{2}$ab=$\frac{1}{2}$��14=7
�ʴ�Ϊ��7��
��3���߾��εı߳��ֱ�Ϊx��y��
�������=xy=��m2-n2����4=$\frac{{m}^{2}-{n}^{2}}{4}$��
�ߴ������εı߳�Ϊm��
��x+y=m��
��С�����εı߳�Ϊn��
��x-y=n��
��x2-y2=��x+y����x-y��=m•n��
��x+y=m��xy=$\frac{{m}^{2}-{n}^{2}}{4}$��
��x2+y2=��x+y��2-2xy=m2-2��$\frac{{m}^{2}-{n}^{2}}{4}$=$\frac{{m}^{2}+{n}^{2}}{2}$��
��������ȷ���У�1����2����3����4����
�ʴ�Ϊ����1����2����3����4����
���� ������Ҫ��������ȫƽ����ʽ�ļ��α����Լ����ɶ�����֤��������ʱע�⣺֤�����ɶ���ʱ���ü���ȫ�ȵ�ֱ��������ƴ��һ�������ͼ�Σ�Ȼ�����ô�ͼ�ε�������ڼ���Сͼ�ε�����ͣ����������õ����ɶ�����

 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�| A�� | -$\frac{1}{2}$ | B�� | -$\frac{\sqrt{2}}{2}$ | C�� | -$\frac{\sqrt{3}}{2}$ | D�� | -$\sqrt{3}$ |
��������ҵ
| �⣺x2-7x+10=0 a=1 b=-7 c=10 ��b2-4ac=9��0 ��x=$\frac{-b��\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{7+3}{2}$ ��x1=5��x2=2 ���ԣ�����Ϊ5����Ϊ2ʱ�����������ε�������Ϊ5��5��2�� ����Ϊ2����Ϊ5ʱ�����������ε�������Ϊ2��2��5�� |
��֪����������ABC�������ǹ���x�ķ���x2-mx+$\frac{m}{2}$-$\frac{1}{4}$=0������ʵ������
��1����m=2ʱ�����ABC���ܳ���
��2������ABCΪ�ȱ�������ʱ����m��ֵ��
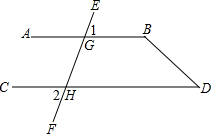 ��ͼ��֪��1=��2����D=50�㣬
��ͼ��֪��1=��2����D=50�㣬 ��ͼ�������������е�ÿ��С�����α߳���Ϊ1��ÿ��С�����εĶ���и�㣬�ֱ�����Ҫ���Ը��Ϊ���������κ�ƽ���ı��Σ�������д������
��ͼ�������������е�ÿ��С�����α߳���Ϊ1��ÿ��С�����εĶ���и�㣬�ֱ�����Ҫ���Ը��Ϊ���������κ�ƽ���ı��Σ�������д������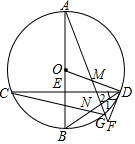 ��ͼ���ڡ�O�У�ֱ��AB������CD���е�E����M��OD�ϣ�AM���ӳ��߽���O�ڵ�G������D��ֱ����F����1=��2������BD��CG���ڵ�N��
��ͼ���ڡ�O�У�ֱ��AB������CD���е�E����M��OD�ϣ�AM���ӳ��߽���O�ڵ�G������D��ֱ����F����1=��2������BD��CG���ڵ�N��