题目内容
11．若k是任意实数，求证：关于x的方程（x-1）（2x-4）=k2有两个相等的实数根．分析 先计算判别式得到△=8k2+4，然后根据非负数的性质得到△＞0，然后根据判别式的意义即可得到结论．
解答 解：原方程可化为2x2-6x+4-k2=0，
∵△=36-4×2×（4-k2）=8k2+4＞0，
∴关于x的方程（x-1）（2x-4）=k2有两个相等的实数根．
点评 此题主要考查了一元二次方程跟的判别式，关键是掌握一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根
练习册系列答案
相关题目
1．若方程2x-kx+1=5x-2的解为x=-1，则k的值为（ ）
| A． | -6 | B． | 10 | C． | -8 | D． | -4 |
2．某商场花了9万元从厂家购买了A型、B型两种型号的电视机共50台，其中A型电视机的进价为每台1500，B型电视机的进价为每台2500元．
（1）若设购买了A型电视机x台，B型电视机y台，请完成下列表格：
（2）在（1）的基础上，通过列二元一次方程组求该商场购买A型和B型电视机各多少台？
（3）若商场A型电视机的售价为每台1700元，B型电视机的售价为每台2800元，不考虑其他因素，那么销售完这50台电视机该商场可获利多少元？
（1）若设购买了A型电视机x台，B型电视机y台，请完成下列表格：
| 进价（元/台） | 购买数量（台） | 购买数量（元） | |
| A型 | 1500 | x | |
| B型 | 2500 | y |
（3）若商场A型电视机的售价为每台1700元，B型电视机的售价为每台2800元，不考虑其他因素，那么销售完这50台电视机该商场可获利多少元？
已知：如图，线段AB=12cm，M是AB上一定点，C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿线段BA向左运动，在运动过程中，点C始终在线段AM上，点D始终在线段BM上，点E、F分别是线段AC和MD的中点．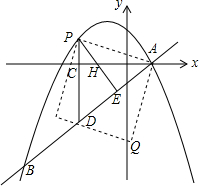
如图，在平面直角坐标系中，直线y=kx+n（k≠0）与抛物线y=-$\frac{1}{4}{x^2}$+bx+c交于A、B两点，点A在x轴上，OA=2，点B的横坐标为-8，且tan∠OAB=$\frac{3}{4}$．
如图，在等边△ABC中，AC=9，点O、P、D分别在AC、AB、BC上，AO=3，OP=OD，且∠DOP=60°，则AP的长是6．