题目内容
6.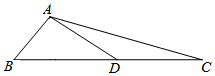 如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是15.
如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是15.
分析 延长AD到点E,使DE=AD=6,连接CE,可证明△ABD≌△CED,所以CE=AB,再利用勾股定理的逆定理证明△CDE是直角三角形即:△ABD为直角三角形,进而可求出△ABD的面积.
解答 解:延长AD到点E,使DE=AD=6,连接CE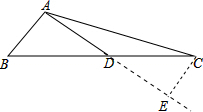 ,
,
∵AD是BC边上的中线,
∴BD=CD,
在△ABD和△CED中,
$\left\{\begin{array}{l}{BD=CD}\\{∠ADB=∠CDE}\\{AD=DE}\end{array}\right.$,
∴△ABD≌△CED(SAS),
∴CE=AB=5,∠BAD=∠E,
∵AE=2AD=12,CE=5,AC=13,
∴CE2+AE2=AC2,
∴∠E=90°,
∴∠BAD=90°,
即△ABD为直角三角形,
∴△ABD的面积=$\frac{1}{2}$AD•AB=15,
故答案为:15.
点评 本题考查了全等三角形的判定和性质、勾股定理的逆定理的运用,解题的关键是添加辅助线,构造全等三角形,题目的设计很新颖,是一道不错的中考题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
17.已知在五边形ABCDE中,∠A+∠B=240°,∠C+∠D=170°,则∠E的度数为( )
| A. | 30° | B. | 110° | C. | 120° | D. | 130° |
 数轴上数a、b的位置如图所示,试比较a与-b的大小关系为:a<-b(填“>”,“<”或“=”).
数轴上数a、b的位置如图所示,试比较a与-b的大小关系为:a<-b(填“>”,“<”或“=”). 如图,三个相同的三角尺拼接成一个图形,请找出图中的所有平行线,并写出完整推理说明平行的理由.
如图,三个相同的三角尺拼接成一个图形,请找出图中的所有平行线,并写出完整推理说明平行的理由.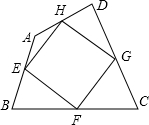 如图,四边形ABCD中,E,F,G,H分别是AB、BC、CD、DA的中点.
如图,四边形ABCD中,E,F,G,H分别是AB、BC、CD、DA的中点.
 如图,直线AB、CD相交于点O,OM⊥AB于点O,若∠MOD=43°,则∠COB=133度.
如图,直线AB、CD相交于点O,OM⊥AB于点O,若∠MOD=43°,则∠COB=133度.