题目内容
14.已知方程x2-4x+2=0得两根为α,β,不解方程求下列各式的值.(1)$\frac{1}{{α}^{2}}$+$\frac{1}{{β}^{2}}$;(2)α2+4β
分析 由根与系数的关系即可得出α+β=4、α•β=2.
(1)将$\frac{1}{{α}^{2}}$+$\frac{1}{{β}^{2}}$变形为$\frac{(α+β)^{2}-2αβ}{(αβ)^{2}}$,再代入数据即可得出结论;
(2)将4替换成α+β,展开后再利用配方法即可将α2+4β变形为(α+β)2-αβ,代入数据即可得出结论.
解答 解:∵方程x2-4x+2=0得两根为α,β,
∴α+β=4,α•β=2.
(1)$\frac{1}{{α}^{2}}$+$\frac{1}{{β}^{2}}$=$\frac{{α}^{2}+{β}^{2}}{{α}^{2}•{β}^{2}}$=$\frac{(α+β)^{2}-2αβ}{(αβ)^{2}}$=$\frac{{4}^{2}-2×2}{{2}^{2}}$=3;
(2)α2+4β=α2+(α+β)•β=α2+β2+αβ=(α+β)2-αβ=42-2=14.
点评 本题考查了根与系数的关系,解题的关键是:(1)将$\frac{1}{{α}^{2}}$+$\frac{1}{{β}^{2}}$变形为$\frac{(α+β)^{2}-2αβ}{(αβ)^{2}}$;(2)将α2+4β变形为(α+β)2-αβ.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列说法不正确的是( )
| A. | 假命题不是命题 | B. | 定理一定是真命题 | ||
| C. | 每个命题都有结论部分 | D. | 有些命题是错误的 |
2.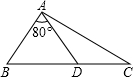 如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C为( )度.
如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C为( )度.
 如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C为( )度.
如图,在△ABC中,点D是BC上一点,∠BAD=80°,AB=AD=DC,则∠C为( )度.| A. | 25 | B. | 30 | C. | 35 | D. | 40 |
3.圆柱共有( )个面.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4.对于反比例函数y=-$\frac{3}{x}$,下列说法不正确的是( )
| A. | 图象经过点(1,-3) | |
| B. | 图象分布在第二、四象限 | |
| C. | 当x>0时,y随x的增大而增大 | |
| D. | 点A(x1,y1)、B(x2、y2)都在反比例函数y=-$\frac{3}{x}$的图象上,若x1<x2,则y1<y2 |
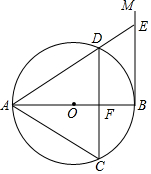 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.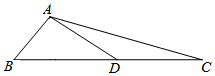 如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是15.
如图,在△ABC中,AB=5,AC=13,BC边上的中线AD=6,则△ABD的面积是15.