题目内容
17.分式方程$\frac{3}{x-2}$-$\frac{x-1}{2-x}$=2的解是x=6.分析 先确定分式方程的最简公分母为(x-2),两边同乘最简公分母将分式方程转化为整式方程求解.
解答 解:$\frac{3}{x-2}$-$\frac{x-1}{2-x}$=2,
去分母,得3+(x-1)=2(x-2),
去括号得3+x-1=2x-4,
合并同类项得-x=-6,
系数化为1得x=6.
经检验x=6是原分式方程的解.
故原分式方程的解是x=6.
故答案为:x=6.
点评 本题主要考查的是分式方程的解法,解分式方程要注意:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.(2)解分式方程一定注意要验根.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.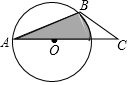 如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )
如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )
 如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )
如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )| A. | 18$\sqrt{2}$+9π | B. | 9$\sqrt{2}$+4.5π | C. | 9$\sqrt{2}$+9π | D. | $\frac{9}{2}$$\sqrt{2}$+4.5π |
9.若关于x的分式方程$\frac{2}{x-3}$+$\frac{x+m}{3-x}$=2-$\frac{2}{x-3}$有增根,则m的值是( )
| A. | m=1 | B. | m=0 | C. | m=3 | D. | m=0或m=3 |
6.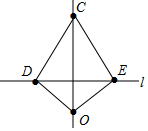 如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
 如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )
如图所示的仪器中,OD=OE,CD=CE.小州把这个仪器往直线l上一放,使点D、E落在直线l上,作直线OC,则OC⊥l,他这样判断的理由是( )| A. | 到一个角两边距离相等的点在这个角的角平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 到线段两端距离相等的点在这条线段的垂直平分线上 | |
| D. | 线段垂直平分线上的点到线段两端的距离相等 |
7.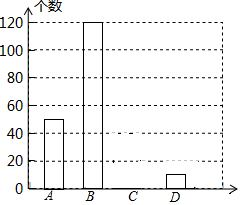 网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
(1)根据上述统计图可得此次采访的人数为200人,a=20,b=0.25;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?
 网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:| 关注情况 | 频数 | 频率 |
| A.高度关注 | 50 | b |
| B.一般关注 | 120 | 0.6 |
| C.不关注 | a | 0.1 |
| D.不知道 | 10 | 0.05 |
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?
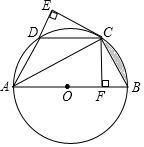 已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD于点E,且CE=CF.
已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD于点E,且CE=CF. 如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题:
如图,在6×6的正方形网格中,每个小正方形顶点叫格点,四边形ABCD的顶点和点Q都在格点上,按要求解答下列问题: