题目内容
8.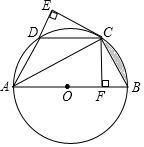 已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD于点E,且CE=CF.
已知:如图,AB是⊙O的直径,C、D为⊙O上两点,CF⊥AB于点F,CE⊥AD于点E,且CE=CF.(1)求证:CE是⊙O的切线;
(2)若AD=CD=6,求图中弧BC与弦BC围成的阴影部分的面积(结果保留π)
分析 (1)连接OC,根据角平分线的判定即可得出∠CAE=∠CAB,由于OC=OA,从而可知∠CAB=∠OCA,所以∠CAE=∠OCA,所以OC∥AE,所以CE是⊙O的切线.
(2)分别求出△OBC与扇形OBC的面积即可求出阴影部分的面积.
解答 解:(1)连接OC,
∵CF⊥AB,CE⊥AD,且CE=CF,
∴∠CAE=∠CAB,
∵OC=OA,
∴∠CAB=∠OCA,
∴∠CAE=∠OCA,
∴OC∥AE,
∴OC⊥CE,
∵OC是⊙O的半径,
∴CE是⊙O的切线;
(2)∵AD=CD,
∴∠DAC=∠DCA=∠CAB,
∴DC∥AB,
∴四边形AODC是平行四边形,
又∵AD=DC,
∴?AODC是菱形,
∴AD=OC=6,
∵∠CAE=∠CAB,
∴$\widehat{CD}=\widehat{CB}$,
∴CD=CB=6,
∴△OCB是等边三角形,
∴∠COB=60°,CF=3$\sqrt{3}$,
∴S△OBC=$\frac{1}{2}$OB•CF=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$,
S扇形OBC=$\frac{60×π×{6}^{2}}{360}$=6π
∴S阴影=S扇形OBC-S△OBC=6π-9$\sqrt{3}$
点评 本题考查圆的综合问题,涉及切线的判定,平行四边形的判定与性质,等边三角形的判定与性质,扇形面积公式等知识,综合程度较高,属于中等题型.

练习册系列答案
相关题目
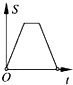
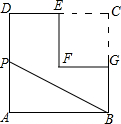 如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )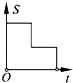
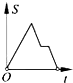
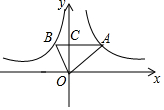 如图,在平面直角坐标系中,点A在函数y=$\frac{3}{x}$ (x>0)的图象上,点B在函数y=$\frac{k}{x}$ (x<0)的图象上,AB⊥y轴于点C.若AC=3BC,则k的值为( )
如图,在平面直角坐标系中,点A在函数y=$\frac{3}{x}$ (x>0)的图象上,点B在函数y=$\frac{k}{x}$ (x<0)的图象上,AB⊥y轴于点C.若AC=3BC,则k的值为( )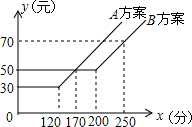 如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论: