题目内容
7.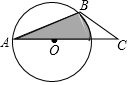 如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )
如图,AB为⊙O的弦,⊙O的切线BC与射线AO交于点C,若∠C=45°,⊙O的半径为6,则图中阴影部分的面积等于( )| A. | 18$\sqrt{2}$+9π | B. | 9$\sqrt{2}$+4.5π | C. | 9$\sqrt{2}$+9π | D. | $\frac{9}{2}$$\sqrt{2}$+4.5π |
分析 如图,连接OB,作OE⊥AB于E,在AE上截取AF=OF,设OE=x,则AF=OF=$\sqrt{2}$x,在Rt△AOE中,利用勾股定理可得62=x2+(x+$\sqrt{2}$x)2,推出x2=9(2-$\sqrt{2}$),根据S阴=S△AOB+S扇形=$\frac{1}{2}$•AB•OE+$\frac{45•π•{6}^{2}}{360}$计算即可.
解答 解:如图,连接OB,作OE⊥AB于E,在AE上截取AF=OF.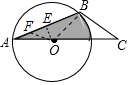
∵BC是切线,
∴BC⊥OB,
∴∠OBC=90°,
∵∠C=45°,
∴∠BOC=∠C=45°,
∴设OE=x,则AF=OF=$\sqrt{2}$x,
在Rt△AOE中,62=x2+(x+$\sqrt{2}$x)2,
∴x2=9(2-$\sqrt{2}$),
∴S阴=S△AOB+S扇形=$\frac{1}{2}$•AB•OE+$\frac{45•π•{6}^{2}}{360}$=$\frac{1}{2}$•2(x+$\sqrt{2}$x)•x+$\frac{9}{2}$π=9$\sqrt{2}$+4.5π.
故选B.
点评 本题考查切线的性质、扇形的面积公式、解直角三角形等知识,解题的关键是学会添加常用辅助线,学会构建方程解决问题,属于中考选择题中的压轴题.

练习册系列答案
相关题目
19.如图是由棱长为1的正方体搭成的某几何体三视图,则图中棱长为1的正方体的个数是( )


| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
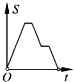
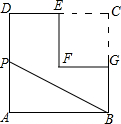 如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )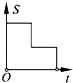
 如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为了测量矗立在高速公路水平地面上的交通警示牌的高度CD,在距M相距4米的A处,测得警示牌下端D的仰角为45°,再笔直往前走8米到达B处,在B处测得警示牌上端C的仰角为30°,求警示牌的高度CD.(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)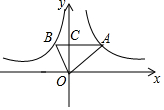 如图,在平面直角坐标系中,点A在函数y=$\frac{3}{x}$ (x>0)的图象上,点B在函数y=$\frac{k}{x}$ (x<0)的图象上,AB⊥y轴于点C.若AC=3BC,则k的值为( )
如图,在平面直角坐标系中,点A在函数y=$\frac{3}{x}$ (x>0)的图象上,点B在函数y=$\frac{k}{x}$ (x<0)的图象上,AB⊥y轴于点C.若AC=3BC,则k的值为( )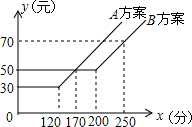 如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论: