题目内容
如果函数y=（a-1）x2+3x+
的图象经过平面直角坐标系的四个象限，那么a的取值范围是 ．
| a+5 |
| a-1 |
考点：抛物线与x轴的交点
专题：
分析：函数图象经过四个象限，需满足3个条件：
（Ⅰ）函数是二次函数；
（Ⅱ）二次函数与x轴有两个交点；
（Ⅲ）两个交点必须要在y轴的两侧，即两个交点异号．
（Ⅰ）函数是二次函数；
（Ⅱ）二次函数与x轴有两个交点；
（Ⅲ）两个交点必须要在y轴的两侧，即两个交点异号．
解答：解：函数图象经过四个象限，需满足3个条件：
（Ⅰ）函数是二次函数．因此a-1≠0，即a≠1①
（Ⅱ）二次函数与x轴有两个交点．因此△=9-4（a-1）
=-4a-11＞0，解得a＜-
②
（Ⅲ）两个交点必须要在y轴的两侧．因此
＜0，解得a＜-5③
综合①②③式，可得：a＜-5．
故答案为：a＜-5．
（Ⅰ）函数是二次函数．因此a-1≠0，即a≠1①
（Ⅱ）二次函数与x轴有两个交点．因此△=9-4（a-1）
| a+5 |
| a-1 |
| 11 |
| 4 |
（Ⅲ）两个交点必须要在y轴的两侧．因此
| a+5 |
| (a-1)2 |
综合①②③式，可得：a＜-5．
故答案为：a＜-5．
点评：本题考查二次函数的图象与性质、二次函数与x轴的交点、二次函数与y轴交点等知识点，解题关键是确定“函数图象经过四个象限”所满足的条件．
练习册系列答案
相关题目
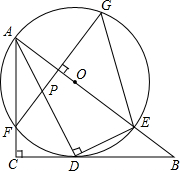如图，在Rt△ABC中，∠C=90°，AD是角平分线，DE⊥AD交AB于E，△ADE的外接圆⊙O与边AC相交于点F，过F作AB的垂线交AD于P，交⊙O于G，连接GE．
如图，在边长为1的小正方形构成的网格中，半径为1的⊙O与大正方形的四个边相切，则图中阴影部分两个小扇形的面积之和为
如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于
如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，点Q为对角线AC上的动点，则△BEQ周长的最小值为