题目内容
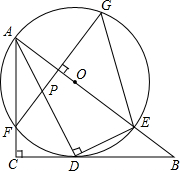 如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.
如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.(1)求证:BC是⊙O的切线;
(2)若tan∠G=
| 4 |
| 3 |
(3)在(2)的条件下,求AP的长.
考点:圆的综合题
专题:
分析:(1)连结OD,根据AD是角平分线,求出∠C=90°,得到OD⊥BC,求出BC是⊙O的切线;
(2)构造直角三角形,根据勾股定理求出k的值即可;
(3)设FG与AE的交点为M,连结AG,利用三角函数和相似三角形结合勾股定理解题.
(2)构造直角三角形,根据勾股定理求出k的值即可;
(3)设FG与AE的交点为M,连结AG,利用三角函数和相似三角形结合勾股定理解题.
解答: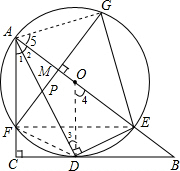 (1)证明:连结OD.
(1)证明:连结OD.
∵DE⊥AD,
∴AE是⊙O的直径,即O在AE上.
∵AD是角平分线,
∴∠1=∠2.
∵OA=OD,
∴∠2=∠3.
∴∠1=∠3.
∴OD∥AC.
∵∠C=90°,
∴OD⊥BC.
∴BC是⊙O的切线.
(2)解:∵OD∥AC,
∴∠4=∠EAF.
∵∠G=∠EAF,
∴∠4=∠G.
∴tan∠4=x=tan∠G=
.
设BD=4k,则OD=OE=3k.
在Rt△OBD中,由勾股定理得(3k)2+(4k)2=(3k+2)2,
解得,k1=1,k2=-
(舍),(注:也可由OB=5k=3k+2得k=1),
∴⊙O的半径为3.
(3)解:设FG与AE的交点为M,连结AG,则∠AGE=90°,∠EGM=∠5.
∴tan∠5=tan∠EGM=
,即
=
=
.
∴
=
,
∴AM=
AE=
.
∵OD∥AC,
∴
=
,
=
,即
=
,
=
.
∴AC=
,CD=
.
∵∠1=∠2,∠2=∠AMP=90°,
∴△ACD∽△AMP.
∴
=
=
,
∴PM=
AM=
.
∴AP=
=
.
 (1)证明:连结OD.
(1)证明:连结OD.∵DE⊥AD,
∴AE是⊙O的直径,即O在AE上.
∵AD是角平分线,
∴∠1=∠2.
∵OA=OD,
∴∠2=∠3.
∴∠1=∠3.
∴OD∥AC.
∵∠C=90°,
∴OD⊥BC.
∴BC是⊙O的切线.
(2)解:∵OD∥AC,
∴∠4=∠EAF.
∵∠G=∠EAF,
∴∠4=∠G.
∴tan∠4=x=tan∠G=
| 4 |
| 3 |
设BD=4k,则OD=OE=3k.
在Rt△OBD中,由勾股定理得(3k)2+(4k)2=(3k+2)2,
解得,k1=1,k2=-
| 1 |
| 4 |
∴⊙O的半径为3.
(3)解:设FG与AE的交点为M,连结AG,则∠AGE=90°,∠EGM=∠5.
∴tan∠5=tan∠EGM=
| 4 |
| 3 |
| GM |
| AM |
| EM |
| GM |
| 4 |
| 3 |
∴
| AM |
| EM |
| 9 |
| 16 |
∴AM=
| 9 |
| 25 |
| 54 |
| 25 |
∵OD∥AC,
∴
| OD |
| AC |
| OB |
| AB |
| CD |
| AO |
| DB |
| OB |
| 3 |
| AC |
| 5 |
| 8 |
| CD |
| 3 |
| 4 |
| 5 |
∴AC=
| 24 |
| 5 |
| 12 |
| 5 |
∵∠1=∠2,∠2=∠AMP=90°,
∴△ACD∽△AMP.
∴
| PM |
| AM |
| CD |
| AC |
| 1 |
| 2 |
∴PM=
| 1 |
| 2 |
| 27 |
| 25 |
∴AP=
| PM2+AM2 |
| 27 |
| 25 |
| 5 |
点评:本题考查了圆的综合题,涉及切线的判定、勾股定理、相似三角形、特殊角的三角函数值,是综合题,要注意全面考虑.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
下面计算(-7+a+b)(-7-a-b)正确的是( )
| A、原式=[-(-7-a-b)][-(7+a+b)]=72-(a+b)2 |
| B、原式=[-(-7+a)+b][-(7+a)-b]=(7+a)2-b2 |
| C、原式=(-7+a+b)[-7-(a+b)]=-72-(a+b)2 |
| D、原式=(-7+a+b)[-7-(a+b)]=72+(a+b)2 |
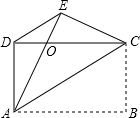 如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.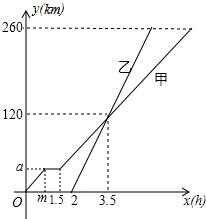
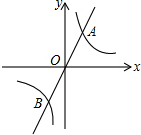 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=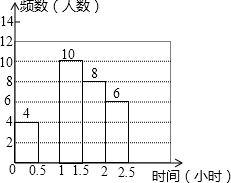 兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.
兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制,规定每天完成家庭作业的时间不超过1.5小时,该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查,并绘制出频数分布表和频数分布直方图(如图)的一部分.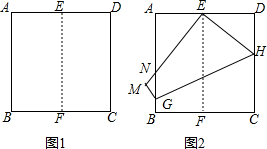 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=
如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=