题目内容
 如图,在边长为1的小正方形构成的网格中,半径为1的⊙O与大正方形的四个边相切,则图中阴影部分两个小扇形的面积之和为
如图,在边长为1的小正方形构成的网格中,半径为1的⊙O与大正方形的四个边相切,则图中阴影部分两个小扇形的面积之和为考点:扇形面积的计算
专题:
分析:先根据直角三角形的性质求出∠ABC+∠BAC的值,再根据扇形的面积公式进行解答即可.
解答: 解:∵△ABC是直角三角形,
解:∵△ABC是直角三角形,
∴∠ABC+∠BAC=90°,
∵两个阴影部分扇形的半径均为1,
∴S阴影=
=
.
故答案为:
.
 解:∵△ABC是直角三角形,
解:∵△ABC是直角三角形,∴∠ABC+∠BAC=90°,
∵两个阴影部分扇形的半径均为1,
∴S阴影=
| 90π×12 |
| 360 |
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:本题考查的是扇形的面积及直角三角形的性质,熟知扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
下列运算中正确的是( )
| A、x+2x=3x2 |
| B、x2•x3=x5 |
| C、x3÷x=3 |
| D、(-x)3=x3 |
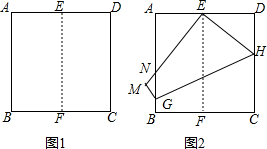 如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=
如图1,将正方形纸片ABCD对折,使AB与CD重合,折痕为EF.如图2,展开后再折叠一次,使点C与点E重合,折痕为GH,点B的对应点为点M,EM交AB于N,则tan∠ANE=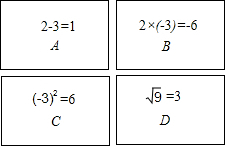 如图,有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个不同的算式,将这四张卡片背面向上洗匀,从中随机抽取两张卡片,这两张卡片上的算式只有一个正确的概率是
如图,有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个不同的算式,将这四张卡片背面向上洗匀,从中随机抽取两张卡片,这两张卡片上的算式只有一个正确的概率是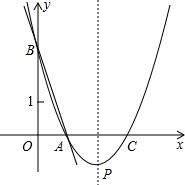 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.