题目内容
如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，点Q为对角线AC上的动点，则△BEQ周长的最小值为考点：轴对称-最短路线问题,正方形的性质
专题：计算题
分析：连接BD，DE，根据正方形的性质可知点B与点D关于直线AC对称，故DE的长即为BQ+QE的最小值，进而可得出结论．
解答：
解：连接BD，DE，
∵四边形ABCD是正方形，
∴点B与点D关于直线AC对称，
∴DE的长即为BQ+QE的最小值，
∵DE=BQ+QE=
=
=5，
∴△BEQ周长的最小值=DE+BE=5+1=6．
故答案为：6．
解：连接BD，DE，∵四边形ABCD是正方形，
∴点B与点D关于直线AC对称，
∴DE的长即为BQ+QE的最小值，
∵DE=BQ+QE=
| AD2+AE2 |
| 42+32 |
∴△BEQ周长的最小值=DE+BE=5+1=6．
故答案为：6．
点评：本题考查的是轴对称-最短路线问题，熟知轴对称的性质是解答此题的关键．
练习册系列答案
相关题目
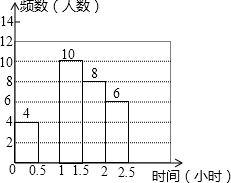兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制，规定每天完成家庭作业的时间不超过1.5小时，该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查，并绘制出频数分布表和频数分布直方图（如图）的一部分．下列运算中正确的是（ ）
| A、x+2x=3x2 |
| B、x2•x3=x5 |
| C、x3÷x=3 |
| D、（-x）3=x3 |
一组数据1，3，6，1，2的众数和中位数分别是（ ）
| A、1，6 | B、1，1 |
| C、2，1 | D、1，2 |
