题目内容
12.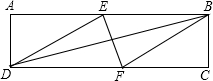 如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:
如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE.现给出下列命题:(1)若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$
(2)若DE2=BD•EF,则DF=2AD
那么,下面判断正确的是( )
| A. | ①正确,②正确 | B. | ①正确,②错误 | C. | ①错误,②正确 | D. | ①错误,②错误 |
分析 ①由已知先求出cos∠BFC=$\frac{\sqrt{3}}{2}$,再求出tan∠EDF,即可判断;
②由S△DEF=$\frac{1}{2}$DF•AD=$\frac{1}{4}$BD•EF,及DE2=BD•EF,可得DF•AD=$\frac{1}{2}$DF2,即DF=2AD.
解答  解:①设CF=x,DF=y,BC=h.
解:①设CF=x,DF=y,BC=h.
∵四边形BFDE是菱形,
∴BF=DF=y,DE∥BF.
∵$\frac{{S}_{矩形ABCD}}{{S}_{四边形BFDE}}$=$\frac{2+\sqrt{3}}{2}$,
∴$\frac{(x+y)h}{yh}$=$\frac{2+\sqrt{3}}{2}$,
∴$\frac{x}{y}$=$\frac{\sqrt{3}}{2}$,即cos∠BFC=$\frac{\sqrt{3}}{2}$,
∴∠BFC=30°,
∵DE∥BF,
∴∠EDF=∠BFC=30°,
∴tan∠EDF=$\frac{\sqrt{3}}{3}$,
所以①是真命题.
②∵四边形BFDE是菱形,
∴DF=DE.
∵S△DEF=$\frac{1}{2}$DF•AD=$\frac{1}{4}$BD•EF,
又∵DE2=BD•EF(已知),
∴S△DEF=$\frac{1}{4}$DE2=$\frac{1}{4}$DF2,
∴DF•AD=$\frac{1}{2}$DF2,
∴DF=2AD,
所以②是真命题.
故选:A.
点评 此题考查了矩形的性质及菱形的性质,解题的关键是①先求出∠EDF的余弦函数值确定其度数,再求出其正切.②用面积法确定.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
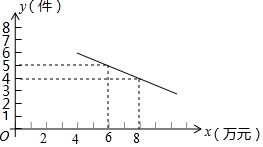 某公司销售某一种新型通讯产品,已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量y(件)与销售单价x (万元)之间存在着如图所示的一次函数关系.
某公司销售某一种新型通讯产品,已知每件产品的进价为4万元,每月销售该种产品的总开支(不含进价)总计11万元.在销售过程中发现,月销售量y(件)与销售单价x (万元)之间存在着如图所示的一次函数关系.
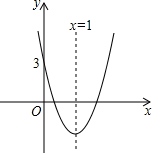 如图,抛物线的对称轴是x=1,与x轴有两个交点,与y轴的交点坐标是(0,3),把它向下平移2个单位长度后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论:
如图,抛物线的对称轴是x=1,与x轴有两个交点,与y轴的交点坐标是(0,3),把它向下平移2个单位长度后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论: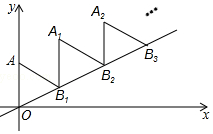 如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019).
如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019). 如图,∠MON及ON上一点A.
如图,∠MON及ON上一点A.
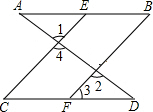 如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C.
如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C.