题目内容
15.某公司开发了一种新产品,现要在甲地或者乙地进行销售,设年销售量为x(件),其中x>0.若在甲地销售,每件售价y(元)与x之间的函数关系式为y=-$\frac{1}{10}$x+100,每件成本为20元,设此时的年销售利润为w甲(元)(利润=销售额-成本).
若在乙地销售,受各种不确定因素的影响,每件成本为a元(a为常数,18≤a≤25 ),每件售价为98元,销售x(件)每年还需缴纳$\frac{1}{10}$x2元的附加费.设此时的年销售利润为w乙(元)(利润=销售额-成本-附加费).
(1)当a=18,且x=100是,w乙=7000元;
(2)求w甲与x之间的函数关系式(不必写出x的取值范围),当w甲=15000时,若使销售量最大,求x的值;
(3)为完成x件的年销售任务,请你通过分析帮助公司决策,应选择在甲地还是在乙地销售才能使该公司所获年利润最大.
分析 (1)根据“乙地销售利润=每件利润×销售量-附加费用”列式计算可得;
(2)根据“销售总利润=每件利润×销售量”列方程解之可得;
(3)先根据(1)中相等关系列出w乙与x之间的函数关系式,再作差得出w甲-w乙=(a-18)x,结合a的取值范围即可判断.
解答 解:(1)当a=18,且x=100时,w乙=(98-18)×100-$\frac{1}{10}$×1002=7000(元),
故答案为:7000;
(2)w甲=x(y-20)=x(-$\frac{1}{10}$x+100-20)=-$\frac{1}{10}$x2+80x,
当w甲=15000时,-$\frac{1}{10}$x2+80x=15000,
解得:x1=300、x2=500,
由于使销售量最大,
故x=500;
(3)∵w乙=-$\frac{1}{10}$x2+(98-a)x,
∴w甲-w乙=-$\frac{1}{10}$x2+80x-[-$\frac{1}{10}$x2+(98-a)x]=(a-18)x,
∵18≤a≤25,且x>0,
∴w甲-w乙>0,即w甲>w乙,
∴应选择在甲地销售.
点评 本题主要考查二次函数的应用,理解题意,确定总利润关于销售量的相等关系,据此列出函数解析式是解题的关键.

练习册系列答案
相关题目
10.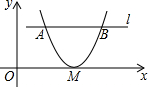 如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
 如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )
如图在平面直角坐标系中,抛物线y=(x-h)2与x轴只有一个交点M,与平行于x轴的直线l交于A,B两点.若AB=3,则点M到直线l的距离为( )| A. | $\frac{5}{2}$ | B. | $\frac{9}{4}$ | C. | 2 | D. | $\frac{7}{4}$ |
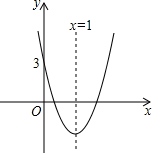 如图,抛物线的对称轴是x=1,与x轴有两个交点,与y轴的交点坐标是(0,3),把它向下平移2个单位长度后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论:
如图,抛物线的对称轴是x=1,与x轴有两个交点,与y轴的交点坐标是(0,3),把它向下平移2个单位长度后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论: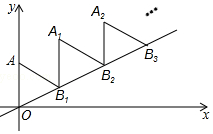 如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019).
如图,放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3…都在直线y=$\frac{\sqrt{3}}{3}$x上,则点A2017的坐标为(2017$\sqrt{3}$,2019).