题目内容
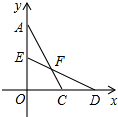 平面直角坐标系中,将两张全等的含90°角的三角形纸片△AOC和△DOE按如图所示摆放在一起,相交于点F.
平面直角坐标系中,将两张全等的含90°角的三角形纸片△AOC和△DOE按如图所示摆放在一起,相交于点F.(1)若直线AC的函数解析式为y=-2x+4,求坐标原点O到直线ED的距离;
(2)在(1)的条件下,连接OF,设点P在x轴上,若△POF是等腰三角形,试求点P的坐标.
考点:一次函数综合题
专题:
分析:(1)由条件可求出OE=OC=2,OD=OA=4,在Rt△OED中由勾股定理可求出线段ED的长度,利用等积法可求出点O到直线ED的距离;
(2)根据待定系数法,可得直线DE的解析式,根据解方程组,可得F点的坐标,根据等腰三角形的定义,可得两边相等,分类讨论:OF=OP,PF=OF,PO=PF,根据两点间的距离公式,可得答案.
(2)根据待定系数法,可得直线DE的解析式,根据解方程组,可得F点的坐标,根据等腰三角形的定义,可得两边相等,分类讨论:OF=OP,PF=OF,PO=PF,根据两点间的距离公式,可得答案.
解答:解:(1)当x=0时,y=4,A(0,4),
当y=0时,-2x+4=0,解得x=2,C(2,0),
OA=4,OC=3,
∵△OAC≌△ODE,
∴OE=OC=2,OD=OA=4,
由勾股定理,得DE=2
,
设O到ED的距离为h,
有三角形的面积,得
DEh=
OE•OD,
即h=
,
解得h=
;
(2)直线DE的解析式为y=kx+b,图象经过(4,0)(0,2),得
,
解得
,
直线DE的解析式为y=
x+2,
F是直线AC与DE的交点,得
,
解得
,
F(
,
).
设P点坐标是(x,0),
①当OF=OP时,|x|=
,即|x|=
,
x=±
,P(
,0),P(-
,0)
②当PF=OF时,
=
,
解得x=
,P(
,0);
③当PO=PF时,|x|=
,
解得x=
,P(
,0),
综上所述:△POF是等腰三角形,点P的坐标是(
,0),(-
,0),(
,0),(
,0).
当y=0时,-2x+4=0,解得x=2,C(2,0),
OA=4,OC=3,
∵△OAC≌△ODE,
∴OE=OC=2,OD=OA=4,
由勾股定理,得DE=2
| 5 |
设O到ED的距离为h,
有三角形的面积,得
| 1 |
| 2 |
| 1 |
| 2 |
即h=
| 2×4 | ||
2
|
解得h=
4
| ||
| 5 |
(2)直线DE的解析式为y=kx+b,图象经过(4,0)(0,2),得
|
解得
|
直线DE的解析式为y=
| 1 |
| 2 |
F是直线AC与DE的交点,得
|
解得
|
F(
| 4 |
| 3 |
| 4 |
| 3 |
设P点坐标是(x,0),
①当OF=OP时,|x|=
(
|
| 4 |
| 3 |
| 2 |
x=±
| 4 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |
②当PF=OF时,
(x-
|
(
|
解得x=
| 8 |
| 3 |
| 8 |
| 3 |
③当PO=PF时,|x|=
(x-
|
解得x=
| 4 |
| 3 |
| 4 |
| 3 |
综上所述:△POF是等腰三角形,点P的坐标是(
| 4 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |
| 8 |
| 3 |
| 4 |
| 3 |
点评:本题考查了一次函数的综合题,利用了全等三角形的性质,三角形的面积公式;等腰三角形的定义,分类讨论是解题关键.

练习册系列答案
相关题目
 如图,E、F分别是线段AC、AB的中点,若EF=20cm,求BC的长.
如图,E、F分别是线段AC、AB的中点,若EF=20cm,求BC的长.