题目内容
已知二次函数y=-x2+bx+c的图象经过点P(0,1)、Q(2,-3).
(1)求此二次函数的解析式;
(2)若点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,且所得四边形ABCD恰为正方形.
①求正方形ABCD的面积;
②连接PA、PD,PD交AB于点E,求证:△PAD∽△PEA.
(1)求此二次函数的解析式;
(2)若点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,且所得四边形ABCD恰为正方形.
①求正方形ABCD的面积;
②连接PA、PD,PD交AB于点E,求证:△PAD∽△PEA.
考点:二次函数综合题
专题:
分析:(1)把点P、Q的坐标代入函数解析式,利用待定系数法求二次函数解析式解答;
(2)①根据二次函数和正方形的对称性可知正方形ABCD关于y轴对称,设点A的坐标为(m,2m),代入二次函数解析式求出m的值,再求出2m,然后根据正方形的面积公式列式计算即可得解;
②设AB与y轴交于点F,根据点A的坐标求出AF、PF,然后利用两边对应成比例,夹角相等两三角形相似求出△APF和△PDO相似,根据相似三角形对应角相等可得∠PAF=∠DPO,再根据两直线平行,内错角相等可得∠DPO=∠ADP,从而得到∠PAF=∠ADP,然后利用两角对应相等,两三角形相似证明即可.
(2)①根据二次函数和正方形的对称性可知正方形ABCD关于y轴对称,设点A的坐标为(m,2m),代入二次函数解析式求出m的值,再求出2m,然后根据正方形的面积公式列式计算即可得解;
②设AB与y轴交于点F,根据点A的坐标求出AF、PF,然后利用两边对应成比例,夹角相等两三角形相似求出△APF和△PDO相似,根据相似三角形对应角相等可得∠PAF=∠DPO,再根据两直线平行,内错角相等可得∠DPO=∠ADP,从而得到∠PAF=∠ADP,然后利用两角对应相等,两三角形相似证明即可.
解答:解:(1)∵二次函数y=-x2+bx+c的图象经过点P(0,1)与Q(2,-3),
∴
,
解得:
,
∴此二次函数的解析式为y=-x2+1;
(2)①如图,∵二次函数图象关于y轴对称,
∴正方形ABCD关于y轴对称,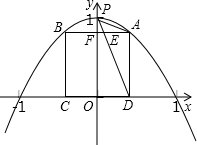
设点A的坐标为(m,2m),则-m2+1=2m,
解得m1=
-1,m2=-
-1(舍去),
∴正方形的边长2m=2
-2,
∴正方形ABCD的面积=(2
-2)2=12-8
;
②证明:设AB与y轴交于点F,
∵A(
-1,2
-2),
∴AF=
-1,PF=1-(2
-2)=3-2
,
∵
=
=
-1,
=
=
-1,
∴
=
,
又∵∠AFP=∠POD,
∴△APF∽△PDO,
∴∠PAF=∠DPO,
∵AD∥y轴,
∴∠DPO=∠ADP,
∴∠PAF=∠ADP,
又∵∠APE=∠DPA,
∴△PAD∽△PEA.
∴
|
解得:
|
∴此二次函数的解析式为y=-x2+1;
(2)①如图,∵二次函数图象关于y轴对称,
∴正方形ABCD关于y轴对称,

设点A的坐标为(m,2m),则-m2+1=2m,
解得m1=
| 2 |
| 2 |
∴正方形的边长2m=2
| 2 |
∴正方形ABCD的面积=(2
| 2 |
| 2 |
②证明:设AB与y轴交于点F,
∵A(
| 2 |
| 2 |
∴AF=
| 2 |
| 2 |
| 2 |
∵
| PF |
| AF |
3-2
| ||
|
| 2 |
| OD |
| OP |
| ||
| 1 |
| 2 |
∴
| PF |
| AF |
| OD |
| OP |
又∵∠AFP=∠POD,
∴△APF∽△PDO,
∴∠PAF=∠DPO,
∵AD∥y轴,
∴∠DPO=∠ADP,
∴∠PAF=∠ADP,
又∵∠APE=∠DPA,
∴△PAD∽△PEA.
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,二次函数的对称轴和正方形的性质,二次函数图象上点的坐标特征,相似三角形的判定与性质,在第②问中求出两三角形的对应边成比例是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果点C是线段AB的黄金分割点(AC>BC),则下列比例式正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
| ||||
| E、? | ||||
| F、? |
 如图,已知△ACE∽△BDE,AC=6,BD=3,AB=12,CD=18.求AE和DE的长.
如图,已知△ACE∽△BDE,AC=6,BD=3,AB=12,CD=18.求AE和DE的长. 已知a,b,c的关系如图所示,化简|a-b|+|a+b|-|c|=
已知a,b,c的关系如图所示,化简|a-b|+|a+b|-|c|=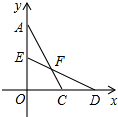 平面直角坐标系中,将两张全等的含90°角的三角形纸片△AOC和△DOE按如图所示摆放在一起,相交于点F.
平面直角坐标系中,将两张全等的含90°角的三角形纸片△AOC和△DOE按如图所示摆放在一起,相交于点F.