题目内容
11.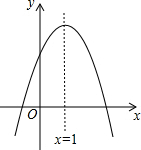 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.
分析 首先把顶点坐标代入函数解析式得到k=a+b+c=$\frac{4}{3}$c,利用c的取值范围可以求得k的取值范围.
解答 解∵抛物线与x轴的一个交点坐标分别是(-1,0),对称轴x=1,
∴抛物线与x轴的另一个交点坐标分别是(3,0),
∴-1×3=-3,
∴$\frac{c}{a}$=-3,则a=-$\frac{c}{3}$.
∵抛物线与y轴的交点在(0,2)、(0,3)之间(不包含端点),
∴2<c<3,
∴-1<-$\frac{c}{3}$<-$\frac{2}{3}$.
∴b=-2a=$\frac{2c}{3}$,
∴k=a+b+c=$\frac{4}{3}$c.
∵2<c<3,
∴$\frac{8}{3}$<$\frac{4}{3}$c<4,即$\frac{8}{3}$<k<4.
故答案为:$\frac{8}{3}$<k<4.
点评 本题考查了二次函数图象与x轴交点坐标与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
2.刘俊问王老师的年龄时,王老师说:“我像你这么大时,你才3岁;等你到了我这么大时,我就45岁了.”设王老师今年x岁,刘俊今年y岁,根据题意,列方程组正确的是( )
| A. | $\left\{\begin{array}{l}x-y=y+3\\ x-y=45+x\end{array}\right.$ | B. | $\left\{\begin{array}{l}x-y=y+3\\ x-y=45-x\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x-y=y-3\\ x-y=45+x\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=y-3\\ x-y=45-x\end{array}\right.$ |
16. 如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶的路程是( )
如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶的路程是( )
 如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶的路程是( )
如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶的路程是( )| A. | 0.5千米 | B. | 1千米 | C. | 1.5千米 | D. | 2千米 |
1.若点A(3,-4)、B(-2,m)在同一个反比例函数的图象上,则m的值为( )
| A. | 6 | B. | -6 | C. | 12 | D. | -12 |
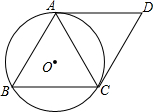 如图,⊙O是△ABC的外接圆,分别过A、C两点作⊙O的两条切线AD、CD,它们的交点为D,且AD∥BC,CD∥AB.
如图,⊙O是△ABC的外接圆,分别过A、C两点作⊙O的两条切线AD、CD,它们的交点为D,且AD∥BC,CD∥AB.
 如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE=$\frac{1}{2}$cm.
如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE=$\frac{1}{2}$cm.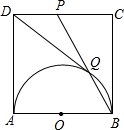 如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②$\frac{PQ}{BQ}$=$\frac{3}{2}$;③S△PDQ=$\frac{1}{8}$;④cos∠ADQ=$\frac{3}{5}$,其中正确结论是①②④(填写序号)
如图,正方形ABCD的边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连结DQ,给出如下结论:①DQ=1;②$\frac{PQ}{BQ}$=$\frac{3}{2}$;③S△PDQ=$\frac{1}{8}$;④cos∠ADQ=$\frac{3}{5}$,其中正确结论是①②④(填写序号)