题目内容
1.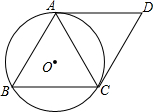 如图,⊙O是△ABC的外接圆,分别过A、C两点作⊙O的两条切线AD、CD,它们的交点为D,且AD∥BC,CD∥AB.
如图,⊙O是△ABC的外接圆,分别过A、C两点作⊙O的两条切线AD、CD,它们的交点为D,且AD∥BC,CD∥AB.(1)试说明四边形ABCD是菱形;
(2)若⊙O的半径是2$\sqrt{3}$,求四边形ABCD的面积.
分析 (1)由AD∥BC,CD∥AB,得到四边形ABCD是平行四边形,根据切线长定理得到AD=CD,于是得到结论;
(2)连接AO、CO,由AD、CD是⊙O的切线,得到∠OAD=∠OCD=90°,由四边形ABCD为菱形,得到∠B=∠D,求出∠B=∠D=60°,得到菱形高为3$\sqrt{3}$,底为6,问题即可得解.
解答 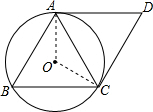 解:(1)∵AD∥BC,CD∥AB,
解:(1)∵AD∥BC,CD∥AB,
∴四边形ABCD是平行四边形,
∵AD、CD是⊙O的切线,
∴AD=CD,
∴四边形ABCD为菱形;
(2)连接AO、CO,
∵AD、CD是⊙O的切线,
∴∠OAD=∠OCD=90°,
∴∠OAD+∠OCD=180°,
∴∠AOC+∠D=180°,
∵四边形ABCD为菱形,
∴∠B=∠D,
∵∠AOC=2∠B,
∴∠B=∠D=60°,
∴菱形高为3$\sqrt{3}$,底为6,
∴S四边形ABCD=18$\sqrt{3}$.
点评 本题主要考查切线的性质及菱形的判定和性质,菱形面积的求法,由切线的性质得到∠OAD=∠OCD=90°是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.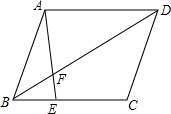 如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
 如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )
如图,在?ABCD中,E为BC边上的点,若BE:EC=4:5,AE交BD于F,则BF:FD等于( )| A. | 4:5 | B. | 3:5 | C. | 4:9 | D. | 3:8 |
16.下列图案中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.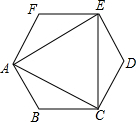 顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
 顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )
顺次连接正六边形的三个不相邻的顶点,得到如图的图形,下列说法错误的是( )| A. | △ACE是等边三角形 | B. | 既是轴对称图形也是中心对称图形 | ||
| C. | 连接AD,则AD分别平分∠EAC与∠EDC | D. | 图中一共能画出3条对称轴 |
10.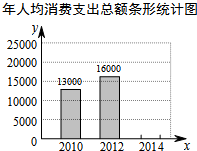 随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
年人均各项消费支出统计表
根据以上信息解答下列问题:
(1)a=5200;并补全条形统计图;
(2)我们把“食品支出总额占个人消费支出总额的百分数”叫做恩格尔系数,请分别求出小明家2010,2012,2014年的恩格尔系数,并根据变化情况谈谈你的看法.
 随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:
随着生活质量的提高,人们的消费水平逐年上升,小明把自己家2010,2012,2014年的消费数据绘制统计图表如下:年人均各项消费支出统计表
| 年份 支出项目(单位:元) | 2010年 | 2012年 | 2014年 |
| 食品支出 | a | 5600 | 6300 |
| 医疗、保健支出 | 2000 | 2200 | 3000 |
| 家庭用品及服务支出 | 3300 | 4000 | 5700 |
| 其他支出 | 2500 | 4200 | 6000 |
(1)a=5200;并补全条形统计图;
(2)我们把“食品支出总额占个人消费支出总额的百分数”叫做恩格尔系数,请分别求出小明家2010,2012,2014年的恩格尔系数,并根据变化情况谈谈你的看法.
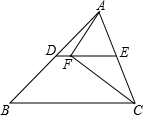 如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为60°.
如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为60°.
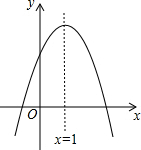 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.