题目内容
6. 如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE=$\frac{1}{2}$cm.
如图,△ABC与△DEF均为等边三角形,⊙O是△ABC的内切圆,同时也是△DEF的外接圆.若AB=1cm,则DE=$\frac{1}{2}$cm.
分析 设AB与⊙O相切于M,连接OB,OM,得到OM⊥AB,由⊙O是等边△ABC的内切圆和等边三角形的性质,求出圆的半径,连接OD,过O作ON⊥OE于N,由⊙O是等边△DEF的外接圆.解直角三角形即可得到结论.
解答  解:设AB与⊙O相切于M,连接OB,OM,
解:设AB与⊙O相切于M,连接OB,OM,
∴OM⊥AB,
∵⊙O是等边△ABC的内切圆
∴∠ABO=30°,OA=OB,
∴BM=$\frac{1}{2}$AB=$\frac{1}{2}$,
∴OM=$\frac{\sqrt{3}}{6}$,
连接OD,过O作ON⊥OE于N,
∵⊙O是等边△DEF的外接圆.
∴OD=OM=$\frac{\sqrt{3}}{6}$,∠ODN=30°,
∴DN=$\frac{1}{4}$,
∴DE=2DN=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了三角形的内切圆和内心,三角形的外接圆和外心,等边三角形的性质,熟练掌握三角形的内切圆和外接圆的性质是解题的关键.

练习册系列答案
相关题目
16.下列图案中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17. 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是( )
如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是( )
 如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是( )
如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是( )| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
 二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有两个不相等的实数根,则整数m的最小值为( )
二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有两个不相等的实数根,则整数m的最小值为( )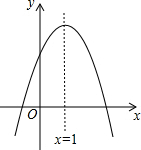 如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4.
如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为C(1,k),与y轴的交点在(0,2)、(0,3)之间(不包含端点),则k的取值范围是$\frac{8}{3}$<k<4. 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下5个结论:
 某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡: