题目内容
13.已知关于x、y的多项式mx2+4xy-x-3x2+2nxy-4y合并后不含有二次项,求n-m的值.分析 由于多项式mx2+4xy-x-2x2+2nxy-4y合并后不含有二次项,即二次项系数为0,在合并同类项时,可以得到二次项为0,由此得到故m、n的方程,即m-3=0,4+2n=0,解方程即可求出m,n,然后把m、n的值代入n-m,即可求出代数式的值.
解答 解:mx2+4xy-x-3x2+2nxy-4y=(m-3)x2+(4+2n)xy-x-4y,
∵合并后不含二次项,
∴m-3=0,4+2n=0,
∴m=3,n=-2,
∴n-m=-2-3=-5.
点评 此题考查了多项式,根据在多项式中不含哪一项,则哪一项的系数为0,由此建立方程,解方程即可求得待定系数的值.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.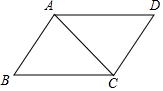 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
 如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )
如图,已知AB∥CD,AD∥CB,则△ABC≌△CDA的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
18.$\frac{2}{3}$的绝对值是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
3.下列各组数相等的是( )
| A. | -32与(-3)2 | B. | -33与(-3)3 | C. | -|-1|与-(-1) | D. | 23与32 |
 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为15cm.
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AB=15cm,则△DBE的周长为15cm. 已知有理数a、b、c在数轴上的位置如图所示,
已知有理数a、b、c在数轴上的位置如图所示,