题目内容
8．
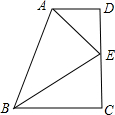如图，梯形ABCD中，AD∥BC，∠D=90°，AE、BE分别是∠DAB和∠ABC的平分线，求证：AB=AD+BC．
分析 作EF⊥AB，根据AAS证明△ADE≌△AFE和△BCE≌△BFE，得到AD=AF，BC=BF，即可证明AB=BC+AD．
解答 证明：作EF⊥AB，
∵AE是∠DAB的平分线，
∴∠DAE=∠FAE，
在△ADE和△AFE中，
$\left\{\begin{array}{l}{∠D=∠AFE=90°}\\{∠DAE=∠FAE}\\{AE=AE}\end{array}\right.$，
∴△ADE≌△AFE（AAS），
∴AD=AF，
同理△BCE≌△BFE，
∴BC=BF，
∵AB=BF+AF．
∴AB=BC+AD
点评 本题主要考查了全等三角形的判定与性质，作EF⊥AB，构造全等三角形是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如右图所示，把两个大小完全一样的矩形拼成“L”形图案，则∠FAC=90°．
如图，已知二次函数y=-x2+bx+8的图象与x轴交于A、B两点，与y轴交于点C，且B（4，0）．
如图，把矩形ABCD折叠，使点C与点A重合，折痕为EF，如果AB=4，BC=8，求BE的长．
平移后过点A（8,0）和原点，顶点为B，对称轴与x轴相交于点C，与原抛物线相交于点D．
；
