题目内容
13.已知a=$\frac{\sqrt{3}+\sqrt{2}}{2}$,b=$\frac{\sqrt{3}-\sqrt{2}}{2}$,求a2+b2的值.分析 分别计算出a+b和ab的值,然后利用完全平方公式即可求出a2+b2的值.
解答 解:∵a+b=$\frac{\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}}{2}$=$\sqrt{3}$,ab=$\frac{\sqrt{3}+\sqrt{2}}{2}$×$\frac{\sqrt{3}-\sqrt{2}}{2}$=$\frac{1}{4}$
∴(a+b)2=($\sqrt{3}$)2=3,
∵(a+b)2=a2+b2+2ab,
∴a2+b2=(a+b)2-2ab=3-$\frac{1}{4}$×2=$\frac{5}{2}$.
点评 本题考查二次根式的化简求出问题,涉及完全平方公式,平方差公式等知识,属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

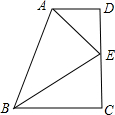 如图,梯形ABCD中,AD∥BC,∠D=90°,AE、BE分别是∠DAB和∠ABC的平分线,求证:AB=AD+BC.
如图,梯形ABCD中,AD∥BC,∠D=90°,AE、BE分别是∠DAB和∠ABC的平分线,求证:AB=AD+BC.