题目内容
1. 如右图所示,把两个大小完全一样的矩形拼成“L”形图案,则∠FAC=90°.
如右图所示,把两个大小完全一样的矩形拼成“L”形图案,则∠FAC=90°.
分析 根据题意可证△AEF≌△CDA,可得AF=AC,∠FAC=90°.
解答 解:∵两个长方形的大小完全相同,
在△AEF和△CDA中
$\left\{\begin{array}{l}{EF=DA}\\{∠AEF=∠CDA}\\{EA=DC}\end{array}\right.$,
∴△AEF≌△CDA (SAS)
∴AF=AC,∠EAF=∠DCA,
又∵∠DCA+∠DAC=90°
∴∠EAF+∠DAC=90°
即∠FAC=90°.
故答案为:90°.
点评 本题考查了全等三角形的判定与性质,理解两个长方形的大小完全相同的含义是解题的关键.

练习册系列答案
相关题目
11.红光运输队欲用A,B,C三种型号的汽车共80辆为某企业一次性将700吨货物从M地运往N地(要求每种型号的汽车都满载),三种型号的汽车的载重量及应获取的运费如表:
设派用A型汽车x辆,B型汽车y辆,红光运输队应获取的总运费为w元.
(1)用含x、y的代数式表示派用的C型汽车的辆数(80-x-y);
(2)求y关于x的函数关系式并直接写出x的取值范围;
(3)求w关于x的函数关系式;
(4)若红光运输队获取的总运费为18600元,请问他们的派车方案是怎样的?
| 汽车型号 | A型 | B型 | C型 |
| 载重量(吨) | 8 | 10 | 12 |
| 运费(元) | 220 | 260 | 280 |
(1)用含x、y的代数式表示派用的C型汽车的辆数(80-x-y);
(2)求y关于x的函数关系式并直接写出x的取值范围;
(3)求w关于x的函数关系式;
(4)若红光运输队获取的总运费为18600元,请问他们的派车方案是怎样的?
 如图所示,已知△ABC,用直尺和圆规作图,作△ABC的高BD、角平分线AE.
如图所示,已知△ABC,用直尺和圆规作图,作△ABC的高BD、角平分线AE.
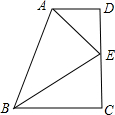 如图,梯形ABCD中,AD∥BC,∠D=90°,AE、BE分别是∠DAB和∠ABC的平分线,求证:AB=AD+BC.
如图,梯形ABCD中,AD∥BC,∠D=90°,AE、BE分别是∠DAB和∠ABC的平分线,求证:AB=AD+BC.