题目内容
19. 如图,已知二次函数y=-x2+bx+8的图象与x轴交于A、B两点,与y轴交于点C,且B(4,0).
如图,已知二次函数y=-x2+bx+8的图象与x轴交于A、B两点,与y轴交于点C,且B(4,0).(1)求二次函数的解析式及其图象的顶点D的坐标;
(2)如果点M(p,0)是x轴上的一个动点,则当|MC-MD|取得最大值时,求p的值;
(3)如果点E(m,n)是二次函数y=-x2+bx+8的图象上的一个动点,且△ABE是钝角三角形,求m的取值范围.
分析 (1)将点B的坐标代入抛物线的解析式得到关于b的方程可求得b的值,从而得到抛物线的解析式,然后利用配方法可求得抛物线的顶点坐标;
(2)当M在直线CD上时,|MC-MD|取得最大值,先求得直线CD的解析式,然后再求得直线CD与x轴的交点坐标,从而得到P的值;
(3)以AB为值经作⊙F,⊙F交抛物线与点E,E′.y=0求得点A和点B的横坐标,然后可确定出圆心F的坐标,设M(x,y)⊙F上的任意一点,依据两点间的距离公式可求得⊙F的解析式,将⊙F的解析式与抛物线的解析式联立可求得点E和E′的坐标,最后依据图形可确定出△ABE为钝角三角形时m的取值范围.
解答 解:(1)将点B的坐标代入得:-16+4b+8=0,解得:b=2,
抛物线的解析式为y=-x2+2x+8.
∵y=-x2+2x+8=-(x-1)2+9,
∴D的坐标为(1,9).
(2)∵当x=0时,y=8,
∴C(0,8).
设直线CD的解析式为y=kx+b.
将点C、D的坐标代入得:$\left\{\begin{array}{l}{b=8}\\{k+b=9}\end{array}\right.$,解得:k=1,b=8,
∴直线CD的解析式为y=x+8.
当y=0时,x+8=0,解得:x=-8,
∴直线CD与x轴的交点坐标为(-8,0).
∵当M在直线CD上时,|MC-MD|取得最大值,
∴点M的坐标为(-8,0).
∴P=-8.
(3)如图所示:以AB为值经作⊙F,⊙F交抛物线与点E,E′.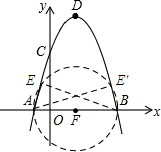
令y=0得:-x2+2x+8=0,解得x=-2或x=4,
∴A(-2,0),B(4,0).
设M(x,y)⊙F上的任意一点.
由两点间的距离公式可知:MF=$\sqrt{(x-1)^{2}+{y}^{2}}$=3,
∴⊙F的解析式为:(x-1)2+y2=9.
将(x-1)2+y2=9与y=-(x-1)2+9联立得:$\left\{\begin{array}{l}{y=-(x-1)^{2}+9}\\{(x-1)^{2}+{y}^{2}=9}\end{array}\right.$
解得:y=0(舍去)或y=1.
将y=1代入抛物线的解析式得:-(x-1)2+9=1,
解得:x=1+2$\sqrt{2}$,或x=1-2$\sqrt{2}$.
∴点E的坐标为(1-2$\sqrt{2}$,1),E′的坐标为(1+2$\sqrt{2}$,1).
根据图图形可知当m<-2或-2<m<1-2$\sqrt{2}$或1+2$\sqrt{2}$<m<4或m>4时,△ABE为钝角三角形.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、两点间的距离公式、解二元二次方程组,明确点点M、C、D在一条直线上时,|MC-MD|取得最大值是解答问题(2)的关键,求得⊙F的解析式是解答问题(3)的关键.

 已知线段a,h(如图),求作等腰三角形ABC,使得底边BC=a,BC边上的高线长为h(保留作图痕迹,不写作法)
已知线段a,h(如图),求作等腰三角形ABC,使得底边BC=a,BC边上的高线长为h(保留作图痕迹,不写作法)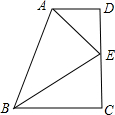 如图,梯形ABCD中,AD∥BC,∠D=90°,AE、BE分别是∠DAB和∠ABC的平分线,求证:AB=AD+BC.
如图,梯形ABCD中,AD∥BC,∠D=90°,AE、BE分别是∠DAB和∠ABC的平分线,求证:AB=AD+BC.