题目内容
16．
如图，把矩形ABCD折叠，使点C与点A重合，折痕为EF，如果AB=4，BC=8，求BE的长．
分析 根据翻折变换的性质可得AE=CE，设BE=x，表示出AE，然后在Rt△ABE中，利用勾股定理列方程求解即可．
解答 解：∵矩形纸片ABCD折叠C点与A点重合，
∴AE=CE，
设BE=x，则AE=8-x，
在Rt△ABE中，由勾股定理得，AB2+BE2=AE2，
即42+x2=（8-x）2，
解得x=3，
即BE=3．
点评 本题考查了翻折变换的性质，主要利用了翻折前后对应线段相等，难点在于利用勾股定理列出方程．
练习册系列答案
相关题目
如图所示，已知△ABC，用直尺和圆规作图，作△ABC的高BD、角平分线AE．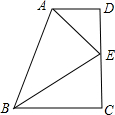
如图，梯形ABCD中，AD∥BC，∠D=90°，AE、BE分别是∠DAB和∠ABC的平分线，求证：AB=AD+BC．