题目内容
6. 如图,等腰Rt△ABC与等腰Rt△BDE中,∠BAC=∠DBE=90°,连接CD、CE,取CD中点F,连接AF,判断AF与CE的数量关系和位置关系,并说明理由.
如图,等腰Rt△ABC与等腰Rt△BDE中,∠BAC=∠DBE=90°,连接CD、CE,取CD中点F,连接AF,判断AF与CE的数量关系和位置关系,并说明理由.
分析 延长CA到M使得AM=AC,连接BM,延长MD、CB交于点N,延长CE交MN于H,由题意AF=$\frac{1}{2}$DM,接下来只要证明△BMD≌△BCE即可.
解答 结论:AF=$\frac{1}{2}$EC,AF⊥EC.
证明:延长CA到M使得AM=AC,连接BM,延长MD、CB交于点N,延长CE交MN于H.
∵∠BAC=90°,
∴BA⊥CM,
∵AM=AC,
∴BM=BC,∠BMC=∠BCM,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠BMC=∠BCM=45°,
∴∠MBC=90°,
∵∠DBE=∠MBC=90°,
∴∠MBD=∠CBE,
在△MBD和△CBE中,
$\left\{\begin{array}{l}{BM=BC}\\{∠MBD=∠CBE}\\{BD=BE}\end{array}\right.$,
∴△MBD≌△CBE,
∴CE=DM,∠BMD=∠BCE,
∵AC=AM,FD=FC,
∴AF∥DM,AF=$\frac{1}{2}$DM,
∴AF=$\frac{1}{2}$DM,
∵∠BMN+∠N=90°,
∴∠BCH+∠N=90°,
∴∠CHN=90°即CH⊥MN,
∵MN∥AF,
∴CH⊥AF.
故AF=$\frac{1}{2}$EC,AF⊥EC.
点评 本题考查全等三角形的判定和性质、三角形中位线定理、等角的余角相等、等腰直角三角形的性质等知识,利用中位线的性质构造辅助线是解决问题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
10.下列计算中正确的是( )
| A. | 3a2+4a=7a3 | B. | 5a3-6a3=-a | C. | a2+3a2=4a2 | D. | 7a-3a=4 |

 已知,如图,在正方形ABCD中,CE垂直于∠CAD的平分线于E,AE交DC于F,求证:CE=$\frac{1}{2}$AF.
已知,如图,在正方形ABCD中,CE垂直于∠CAD的平分线于E,AE交DC于F,求证:CE=$\frac{1}{2}$AF.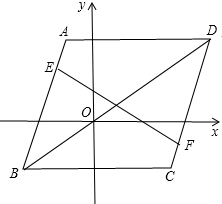 如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD).
如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD). 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=66°.
如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=66°. 如图,已知∠AOB=60°,∠AOC=∠BOC,OD是∠COB的角平分线,求∠COD的度数.
如图,已知∠AOB=60°,∠AOC=∠BOC,OD是∠COB的角平分线,求∠COD的度数.