题目内容
1. 已知,如图,在正方形ABCD中,CE垂直于∠CAD的平分线于E,AE交DC于F,求证:CE=$\frac{1}{2}$AF.
已知,如图,在正方形ABCD中,CE垂直于∠CAD的平分线于E,AE交DC于F,求证:CE=$\frac{1}{2}$AF.
分析 延长AD、CE交于点M,先证明△ADF≌△CDM得AF=CM,再证明△AEC≌△AEM得EC=EM即可得到结论.
解答 证明: 延长AD、CE交于点M,
延长AD、CE交于点M,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=∠CDM=90°,
∵∠EAM+∠M=90°,∠DCM+∠M=90°,
∴∠EAM=∠DCM,
在△ADF和△CDM中,
$\left\{\begin{array}{l}{∠DAF=∠DCM}\\{∠ADF=∠CDM}\\{AD=CD}\end{array}\right.$,
∴△ADF≌△CDM,
∴AF=CM,
在△AEC和△AEM中,
$\left\{\begin{array}{l}{∠EAM=∠EAC}\\{AE=AE}\\{∠AEC=∠AEM}\end{array}\right.$,
∴△AEC≌△AEM,
∴EC=EM,
∴CE=$\frac{1}{2}$AF.
点评 本题考查正方形的性质、角平分线的性质等知识,构造全等三角形是解题的关键.

练习册系列答案
相关题目
 与三角形的一边和其他两边的延长线都相切的圆叫做这个三角形的旁切圆,其圆心叫做这个三角形的旁心.如图,△ABC的三个顶点的坐标分别为A(-3,0),B(3,0),C(0,4).则△ABC位于第二象限的旁心D的坐标是(-5,4).
与三角形的一边和其他两边的延长线都相切的圆叫做这个三角形的旁切圆,其圆心叫做这个三角形的旁心.如图,△ABC的三个顶点的坐标分别为A(-3,0),B(3,0),C(0,4).则△ABC位于第二象限的旁心D的坐标是(-5,4). 如图,在等腰直角△ABC中,AC=BC,AD⊥AB(点D在AB的右上方),E为AB边上一点,且BE=4,DE=6,当CD平分∠ADE时,CE的长度为2$\sqrt{6}$.
如图,在等腰直角△ABC中,AC=BC,AD⊥AB(点D在AB的右上方),E为AB边上一点,且BE=4,DE=6,当CD平分∠ADE时,CE的长度为2$\sqrt{6}$. 如图,等腰Rt△ABC与等腰Rt△BDE中,∠BAC=∠DBE=90°,连接CD、CE,取CD中点F,连接AF,判断AF与CE的数量关系和位置关系,并说明理由.
如图,等腰Rt△ABC与等腰Rt△BDE中,∠BAC=∠DBE=90°,连接CD、CE,取CD中点F,连接AF,判断AF与CE的数量关系和位置关系,并说明理由.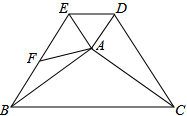 如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.
如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.