题目内容
18. 如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=66°.
如图,AB=CD,AC=DB,∠ABD=25°,∠AOB=82°,则∠DCB=66°.
分析 由AB=CD,AC=DB,易证得△ABC≌△DCB(SSS),然后由全等三角形的对应角相等,求得∠DBC的度数,继而求得答案.
解答 解:在△ABC和△DCB中,
$\left\{\begin{array}{l}{AB=CD}\\{AC=DB}\\{BC=CB}\end{array}\right.$,
∴△ABC≌△DCB(SSS),
∴∠ACB=∠DBC,∠ABC=∠DCB,
∵∠AOB=82°,∠AOB=∠ACB+∠DBC,
∴∠DBC=41°,
∴∠DCB=∠ABC=∠ABD+∠DBC=25°+41°=66°.
故答案为:66°.
点评 此题考查了全等三角形的判定与性质.注意证得△ABC≌△DCB是关键.

练习册系列答案
相关题目
3. 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一点P,作PE⊥PD交AB于点E,与线段AB交于点E,则线段PC的范围是( )
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一点P,作PE⊥PD交AB于点E,与线段AB交于点E,则线段PC的范围是( )
 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一点P,作PE⊥PD交AB于点E,与线段AB交于点E,则线段PC的范围是( )
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=9,BC=12,AB=10,在线段BC上任取一点P,作PE⊥PD交AB于点E,与线段AB交于点E,则线段PC的范围是( )| A. | PC>0 | B. | 0<PC<12 | C. | 3≤PC≤12 | D. | 3<PC<12 |
8.如果等边三角形的边长为8,那么等边三角形三边的中点连接而成的三角形的周长为( )
| A. | 12 | B. | 14 | C. | 16 | D. | 24 |
 如图,等腰Rt△ABC与等腰Rt△BDE中,∠BAC=∠DBE=90°,连接CD、CE,取CD中点F,连接AF,判断AF与CE的数量关系和位置关系,并说明理由.
如图,等腰Rt△ABC与等腰Rt△BDE中,∠BAC=∠DBE=90°,连接CD、CE,取CD中点F,连接AF,判断AF与CE的数量关系和位置关系,并说明理由.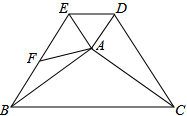 如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.
如图,在△ABC和△ADE中,AB=AC,∠ADE=∠AED,∠BAC+∠EAD=180°,BE,CD,F为BE的中点,连接AF,当∠BAE=90°时,求证:CD=2AF.