题目内容
19.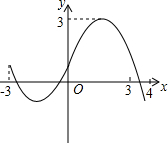 若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任意两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.如下图所表示的函数的界高为4.
若y是关于x的函数,H是常数(H>0),若对于此函数图象上的任意两点(x1,y1),(x2,y2),都有|y1-y2|≤H,则称该函数为有界函数,其中满足条件的所有常数H的最小值,称为该函数的界高.如下图所表示的函数的界高为4.(1)若一次函数y=kx+1(-2≤x≤1)的界高为4,求k的值;
(2)已知m>-2,若函数y=x2(-2≤x≤m)的界高为4,求实数m的取值范围.
分析 (1)根据界高的定义,列出绝对值方程即可解决问题;
(2)根据界高的定义,推出y的最小值以及最大值,即可解决问题;
解答 解:(1)由题意:|-2k+1-(k+1)|=4,
∴|-3k|=4,
∴k=$±\frac{4}{3}$.
(2)∵y的最小值为0,∴y的最大值为4,
将y=4代入抛物线的解析式得:x2=4,解得:x1=-2,x2=2,
,∴m的取值范围是0≤m≤2.
点评 本题考查一次函数、二次函数、绝对值方程等知识,解题的关键是理解题意,把问题转化为绝对值方程解决,体现了数形结合的思想,属于中考常考题型.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
9. 如图,△ABC绕A逆时针旋转使得C点落在BC边上的F处,则对于结论:
如图,△ABC绕A逆时针旋转使得C点落在BC边上的F处,则对于结论:
①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,
其中正确结论的个数是( )
 如图,△ABC绕A逆时针旋转使得C点落在BC边上的F处,则对于结论:
如图,△ABC绕A逆时针旋转使得C点落在BC边上的F处,则对于结论:①AC=AF;②∠FAB=∠EAB;③EF=BC;④∠EAB=∠FAC,
其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
9.为了解学校九年级学生某次知识问卷的得分情况,小红随机调查了50名九年级同学,结果如下表:
则这50名同学问卷得分的众数是 ( )
| 知识问卷得分(单位:分) | 65 | 70 | 75 | 80 | 85 |
| 人数 | 1 | 15 | 15 | 16 | 3 |
| A. | 15 | B. | 16 | C. | 80 | D. | 72.5 |