题目内容
4. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )| A. | ①,② | B. | ①,④ | C. | ③,④ | D. | ②,③ |
分析 确定有关平行四边形,关键是确定平行四边形的四个顶点,由此即可解决问题.
解答 解:∵ 只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
点评 本题考查平行四边形的定义以及性质,解题的关键是理解如何确定平行四边形的四个顶点,四个顶点的位置确定了,平行四边形的大小就确定了,属于中考常考题型.

练习册系列答案
相关题目
9.下列各式属于最简二次根式的是( )
| A. | $\sqrt{18}$ | B. | -$\frac{1}{2}\sqrt{3}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | $\sqrt{\frac{1}{5}}$ |
16.适合下列条件的△ABC中,∠A,∠B,∠C是三个内角,a,b,c分别是∠A,∠B,∠C的对边,直角三角形的个数是( )
①a=7,b=24,C=25;
②a=1.5,b=2,c=7.5;
③∠A:∠B:∠C=1:2:3.
④a=1,b=$\sqrt{2}$,c=$\sqrt{3}$.
①a=7,b=24,C=25;
②a=1.5,b=2,c=7.5;
③∠A:∠B:∠C=1:2:3.
④a=1,b=$\sqrt{2}$,c=$\sqrt{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.已知一次函数y=(1+2m)x-1中,函数值y随自变量x的增大而减小,那么m取值范围是( )
| A. | m<-$\frac{1}{2}$ | B. | m≥-$\frac{1}{2}$ | C. | m≤-$\frac{1}{2}$ | D. | m>-$\frac{1}{2}$ |
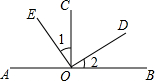 如图,点A,O,B在一条直线上,∠AOC=∠BOC=90°,∠1=∠2,则图中互余的角共有4对.
如图,点A,O,B在一条直线上,∠AOC=∠BOC=90°,∠1=∠2,则图中互余的角共有4对.