题目内容
10.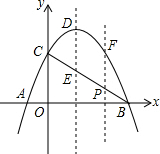 已知抛物线y=-x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且顶点为D(1,4).
已知抛物线y=-x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且顶点为D(1,4).(1)求b和c的值;
(2)如图,连接BC,与抛物线的对称轴相交于点E,点P是线段BC上一动点,作点P作PF∥DF,交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求当四边形DEPF为平行四边形时m的值;
②设△BCF的面积为S,求S与m的函数关系式,并求出s的最大值.
分析 (1)设出二次函数的顶点式,代入顶点坐标即可求得b、c的值;
(2)①PF的长就是当x=m时,抛物线的值与直线BC所在一次函数的值的差.可先根据B,C的坐标求出BC所在直线的解析式,然后将m分别代入直线BC和抛物线的解析式中,求得出两函数的值的差就是PF的长.
根据直线BC的解析式,可得出E点的坐标,根据抛物线的解析式可求出D点的坐标,然后根据坐标系中两点的距离公式,可求出DE的长,然后让PF=DE,即可求出此时m的值.
②可将三角形BCF分成两部分来求:
一部分是三角形PFC,以PF为底边,以P的横坐标为高即可得出三角形PFC的面积.
一部分是三角形PFB,以PF为底边,以P、B两点的横坐标差的绝对值为高,即可求出三角形PFB的面积.
然后根据三角形BCF的面积=三角形PFC的面积+三角形PFB的面积,可求出关于S、m的函数关系式,配方后即可确定最大值.
解答 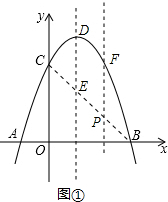 解:(1)设y=-x2+bx+c=-(x-h)2+k,
解:(1)设y=-x2+bx+c=-(x-h)2+k,
∵顶点为D(1,4),
∴y=-x2+bx+c=-(x-1)2+4=-x2+2x+3,
∴b=2,c=3;
(2)令y=0,则-x2+2x+3=-(x+1)(x-3)=0,
解得,x=-1或x=3,则A(-1,0),B(3,0).
令x=0,则y=0,则C(0,3).
综上所述,A(-1,0),B(3,0),C(0,3),抛物线的对称轴是x=1;
①设直线BC的函数关系式为:y=kx+b(k≠0).
把B(3,0),C(0,3)分别代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:k=-1,b=3.
所以直线BC的函数关系式为:y=-x+3.
当x=1时,y=-1+3=2,
∴E(1,2).
当x=m时,y=-m+3,
∴P(m,-m+3).
在y=-x2+2x+3中,当x=1时,y=4.
∴D(1,4)
当x=m时,y=-m2+2m+3,
∴F(m,-m2+2m+3)
∴线段DE=4-2=2,
线段PF=-m2+2m+3-(-m+3)=-m2+3m ∵PF∥DE,
∵PF∥DE,
∴当PF=ED时,四边形PEDF为平行四边形.
由-m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).
因此,当m=2时,四边形PEDF为平行四边形.
②设直线PF与x轴交于点M,由B(3,0),O(0,0),可得:OB=OM+MB=3.
S=S△BCF=S△BPF+S△CPF=$\frac{1}{2}$FP•OM+$\frac{1}{2}$FP•BM=$\frac{1}{2}$(-m2+3m)×3=-$\frac{3}{2}$m2+$\frac{9}{2}$m=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{27}{8}$.
∴S的最大值为$\frac{27}{8}$.
点评 本题主要考查了二次函数的综合应用,根据二次函数得出相关点的坐标和对称轴的解析式是解题的基础.

 阅读快车系列答案
阅读快车系列答案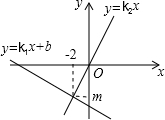 同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )
同一平面直角坐标系中,一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示,则关于x的方程k1x-2b>k2x的解为( )| A. | x>-2 | B. | x<-2 | C. | x<2 | D. | x<4 |
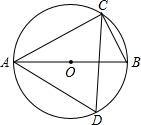 如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )
如图,AB是⊙O的直径,C、D在圆上,且∠BAC=28°,则∠ADC=( )| A. | 52° | B. | 56° | C. | 62° | D. | 72° |
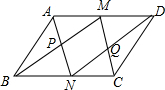 如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )
如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是( )| A. | AP=PN | B. | NQ=QD | ||
| C. | 四边形PQNM是矩形 | D. | △ABN是等边三角形 |
 如图,现下由三个语句:
如图,现下由三个语句: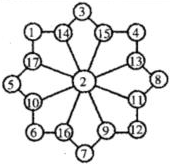 如图,在17个小圆圈里分别填写着1至17这些自然数,每个小四边形上的4个数字之和都是34.想想看,如何调整一下这些数,使每个小四边形上的数字之和变为38?
如图,在17个小圆圈里分别填写着1至17这些自然数,每个小四边形上的4个数字之和都是34.想想看,如何调整一下这些数,使每个小四边形上的数字之和变为38?